【题目】(10分)在Rt△ABC中,∠BAC=![]() ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.

(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
参考答案:
【答案】(1)证明详见解析;(2)证明详见解析;(3)10.
【解析】
试题(1)由∠DBE=∠AFE,∠BED=∠FEA,ED=EA,根据“AAS”证得△BDE≌△FAE(AAS);
(2)由全等可得AF=BD,即AF=DC,根据一组对边平行且相等的四边形的平行四边形证得四边形ADCF是平行四边形,又邻边AD=DC,所以四边形四边形ADCF是菱形;
(3)解法一:连接DF,证得四边形ABDF是平行四边形,从而得到对角线DF的长,利用菱形的对角线长求面积;
解法二:利用Rt△ABC的面积求得BC边上的高,即得到菱形ADCF中DC边上的高,利用平行四边形的面积公式求菱形的面积.
试题解析:(1)证明:在Rt△ABC中,∠BAC=![]() ,D是BC的中点,
,D是BC的中点,
∴AD=![]() BC=DC=BD,
BC=DC=BD,
∵AF∥BC,
∴∠DBE=∠AFE,
又∵E是AD中点,
∴ED=EA,
又∠BED=∠FEA,
∴△BDE≌△FAE(AAS);
(2)证明:由(1)知AF=BD,即AF=DC,
∴AF∥DC,AF=DC,
∴四边形ADCF是平行四边形,
又∵AD=DC,
∴四边形ADCF是菱形;
(3)解:(解法一)连接DF,
∵AF![]() DC,BD=CD,
DC,BD=CD,
∴AF![]() BD,
BD,
∴四边形ABDF是平行四边形,
∴DF=AB=5,
∴![]() ;
;
(解法二)在Rt△ABC中,AC=4,AB=5,
∴BC=![]() ,
,
设BC边上的高为![]() ,
,
则![]() ,
,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一副三角板,
(1)按如图①所示方式放置,点
 三点共线,
三点共线, ,求
,求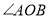 的度数;
的度数;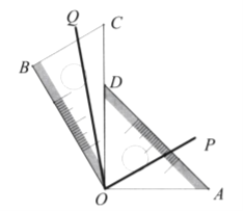
(2)在(1)的条件下,若
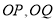 分别是
分别是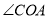 与
与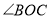 内部的一条射线,且
内部的一条射线,且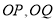 均以点
均以点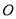 为中心,分别从
为中心,分别从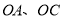 位置出发,以
位置出发,以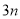 度/秒、
度/秒、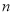 度/秒的旋转速度沿逆时针方向旋转,当
度/秒的旋转速度沿逆时针方向旋转,当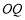 与
与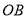 重叠时,所有旋转均停止,试说明:当旋转
重叠时,所有旋转均停止,试说明:当旋转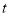 秒后,
秒后,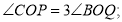
(3)若三角板
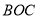 (不含
(不含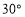 角)是一块非标准三角板,按如图②所示方式放置,使
角)是一块非标准三角板,按如图②所示方式放置,使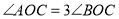 ,作射线
,作射线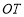 ,若
,若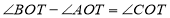 ,求
,求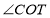 与
与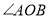 的度数之比.
的度数之比.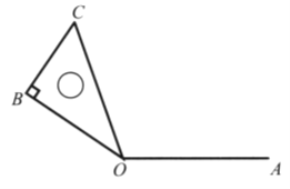
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=70°,∠BCD=40°,则∠BED的度数为______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,A(0,4),C(2,0).
(1)画出线段AC关于y轴的对称线段AB;
(2)将线段CA绕点C顺时针旋转一个角,得到对应的线段CD,使得AD∥x轴,请画出线段CD;
(3)若直线y=kx平分四边形ABCD的面积,请求出k的值. -
科目: 来源: 题型:
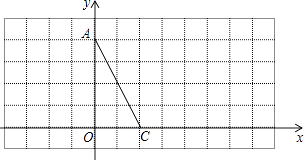
查看答案和解析>>【题目】如图,直线AB与直线BC交于B点,∠ABC=n°(n>110),直线EF与直线AB交于点G,与直线BC交于H点,∠AGE=70°,将EF向右平移,在平移的过程中,∠GHC=_______°(用含n的式子表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,已知AB=CD,点E、F分别为AD、BC的中点,延长BA、CD,分别交射线FE于P、Q两点.求证:∠BPF=∠CQF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,AC∥BE,∠MAC=40,∠D=50°,CH平分∠ACD,BH平分∠ABD,
(1)求∠EBH的角度
(2)求∠BHC的角度

相关试题

