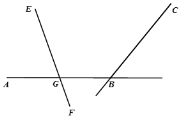
【题目】如图,直线AB与直线BC交于B点,∠ABC=n°(n>110),直线EF与直线AB交于点G,与直线BC交于H点,∠AGE=70°,将EF向右平移,在平移的过程中,∠GHC=_______°(用含n的式子表示)
参考答案:
【答案】n-70或250-n
【解析】
根据三角形外角的性质,分当H在直线AB下方时,当H在直线AB上方时两种情况解答即可.
解:在平移过程中,
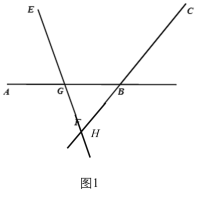
当H在直线AB下方时,如图,
∵∠ABC=∠GHC+∠HGB=∠GHC+∠AGE,∠AGE=70°,∠ABC=n°,
∴∠GHC=∠ABC-∠AGE=n°-70°;
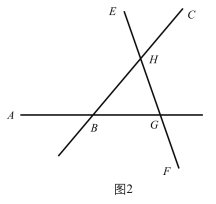
当H在直线AB上方时,如图,
∵∠ABC=∠AGE +∠BHG,
∠GHC=∠AGE+∠CBG,
∠AGE=70°,∠ABC=n°,
∴∠ABC+∠GHC=∠AGE +∠BHG+∠AGE+∠CBG=180°+∠AGE=180°+70°=250°,
∴∠GHC=∠ABC-∠AGE=250°-n°;
故答案为:n-70或250-n.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=70°,∠BCD=40°,则∠BED的度数为______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,A(0,4),C(2,0).
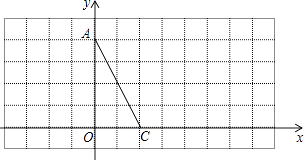
(1)画出线段AC关于y轴的对称线段AB;
(2)将线段CA绕点C顺时针旋转一个角,得到对应的线段CD,使得AD∥x轴,请画出线段CD;
(3)若直线y=kx平分四边形ABCD的面积,请求出k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)在Rt△ABC中,∠BAC=
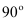 ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,已知AB=CD,点E、F分别为AD、BC的中点,延长BA、CD,分别交射线FE于P、Q两点.求证:∠BPF=∠CQF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,AC∥BE,∠MAC=40,∠D=50°,CH平分∠ACD,BH平分∠ABD,
(1)求∠EBH的角度
(2)求∠BHC的角度

-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是小东设计的“作
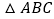 中
中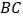 边上的高线”的尺规作图过程.
边上的高线”的尺规作图过程.已知:
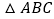 .
. 求作:
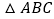 中
中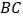 边上的高线
边上的高线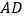 .
.作法:如图,
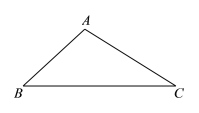
①以点
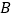 为圆心,
为圆心,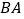 的长为半径作弧,以点
的长为半径作弧,以点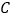 为圆心,
为圆心,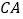 的长为半径作弧,两弧在
的长为半径作弧,两弧在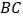 下方交于点
下方交于点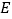 ;
;②连接
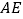 交
交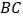 于点
于点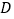 .
.所以线段
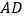 是
是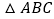 中
中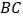 边上的高线.
边上的高线.根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵
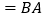 ,
, 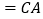 ,
,∴点
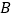 ,
,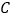 分别在线段
分别在线段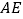 的垂直平分线上( )(填推理的依据).
的垂直平分线上( )(填推理的依据).∴
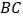 垂直平分线段
垂直平分线段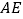 .
. ∴线段
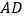 是
是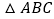 中
中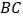 边上的高线.
边上的高线.
相关试题

