【题目】如图,已知AD、AE分别是△ABC的中线、高,且AB=4cm,AC=3cm,请解答下列问题:
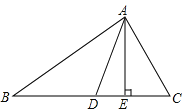
(1)△ABD与△ACD的面积大小有怎样的关系?并说明理由.
(2)△ABD与△ACD的周长之差是多少?
(3)当AE=2.5cm ,BC=6cm时,试求△ABD的面积.
参考答案:
【答案】(1)△ABD和△ACD的面积相等,理由见解析;(2)1 ;(3)S△ABD=3.75 cm2
【解析】
(1)根据三角形面积公式即可比较判断;
(2)根据周长的定义即可比较判断;
(3)根据三角形的面积公式代入即可求解.
(1)△ABD和△ACD的面积相等,
理由如下:
∵AD、AE分别是△ABC的中线和高
∴BD=CD
S△ABD=![]() ,S△ACD=
,S△ACD=![]()
∴S△ABD= S△ACD
(2)△ABD的周长=AB+BD+AD=4+BD+AD
△ACD的周长=AC+DC+AD=3+DC+AD
∵BD=DC
∴(4+BD+AD)-(3+DC+AD)
=1
(3)当AE=2.5 cm,BC=6 cm时,BD=![]() BC=3cm
BC=3cm
∴S△ABD=![]() =
=![]() =3.75 cm2
=3.75 cm2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
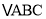 中,
中,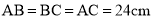 ,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为
,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为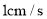 ,点N的速度为
,点N的速度为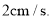 当点N第一次到达B点时,M、N同时停止运动.
当点N第一次到达B点时,M、N同时停止运动.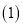 点M,N运动几秒后,M、N两点重合?
点M,N运动几秒后,M、N两点重合? 点M、N运动几秒后,可得到等边三角形
点M、N运动几秒后,可得到等边三角形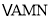 ?
? 当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时M、N运动的时间.
当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时M、N运动的时间.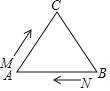
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)当∠BDA=115°时,∠EDC= °,∠DEC= °;点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某工程队在我市实施棚户区改造过程中承包了一项拆迁工程.原计划每天拆迁
 ,因为准备工作不足,第一天少拆迁了
,因为准备工作不足,第一天少拆迁了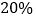 .从第二天开始,该工程队加快了拆迁速度,第三天拆迁了
.从第二天开始,该工程队加快了拆迁速度,第三天拆迁了 .求:
.求: 该工程队第一天拆迁的面积;
该工程队第一天拆迁的面积; 若该工程队第二天、第三天每天的拆迁面积比前一天增加的百分数相同,求这个百分数.
若该工程队第二天、第三天每天的拆迁面积比前一天增加的百分数相同,求这个百分数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH与BE相交于点G.
(1)求证:BF=AC;
(2)求证:CE=
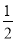 BF.
BF.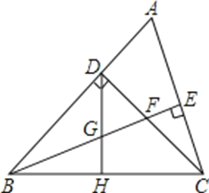
-
科目: 来源: 题型:
查看答案和解析>>【题目】要建一个如图所示的面积为300
 的长方形围栏,围栏总长50m,一边靠墙(墙长25m),
的长方形围栏,围栏总长50m,一边靠墙(墙长25m),
(1)求围栏的长和宽;
(2)能否围成面积为400
 的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由。
的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】五一期间,小明一家一起去旅游,如图是小明设计的某旅游景点的图纸(网格是由相同的小正方形组成的,且小正方形的边长代表实际长度100m),在该图纸上可看到两个标志性景点A,B.若建立适当的平面直角坐标系,则点A(-3,1),B(-3,-3),第三个景点C(3,2)的位置已破损.
(1)请在图中标出景点C的位置;
(2)小明想从景点B开始游玩,途经景点A,最后到达景点C,求小明一家最短的行走路程(参考数据:
 ≈6,结果保留整数).
≈6,结果保留整数).
相关试题

