搜索
【题目】终身学习是学习型社会的核心内容，努力建设“学习型家庭”也是一个重要组成部分．为了解“学习型家庭”情况，某社区对部分家庭六月份的平均每天看书学习时间进行了一次抽样调查，并根据收集的数据绘制了下面两幅不完整的统计图，请根据图中提供的信息，解答下列问题：
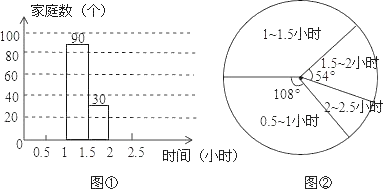
（1）本次抽样调查了多少个家庭；
（2）将图①中的条形图补充完整；
（3）学习时间在1～1.5小时的部分对应的扇形圆心角的度数是多少；
（4）若该社区有家庭有5000个，请你估计该社区学习时间不少于1小时的约有多少个家庭？
参考答案：
【答案】（1）200个；（2）补图见解析；（3）108°；（4）3500个.
【解析】
（1）根据1.5～2小时的圆心角度数求出1.5～2小时所占的百分比，再用1.5～2小时的人数除以所占的百分比，即可得出本次抽样调查的总家庭数；
（2）用抽查的总人数乘以学习0.5-1小时的家庭所占的百分比求出学习0.5-1小时的家庭数，再用总人数减去其它家庭数，求出学习2-2.5小时的家庭数，从而补全统计图；
（3）用360°乘以学习时间在1～1.5小时所占的百分比，即可求出学习时间在1～1.5小时的部分对应的扇形圆心角的度数；
（4）用该社区所有家庭数乘以学习时间不少于1小时的家庭数所占的百分比即可得出答案．
（1）本次抽样调查的家庭数是：30÷
=200（个）；
故答案为：200；
（2）学习0.5-1小时的家庭数有：200×
=60（个），
学习2-2.5小时的家庭数有：200-60-90-30=20（个），
补图如下：
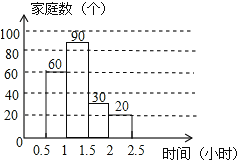
（3）学习时间在1～1.5小时的部分对应的扇形圆心角的度数是：360×
=108°；
故答案为：108；
（4）根据题意得：5000×
=3500（个）．
答：该社区学习时间不少于1小时的家庭约有3500个．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）如图，∠1＝75°，∠2＝105°，∠C＝∠D．判断 ∠A与 ∠F的大小关系，并说明理由．
（2）对于某些数学问题，灵活运用整体思想，可以化难为易．在解二元一次方程组时，就可以运用整体代入法：如解方程组：
.解：把②代入①得，
解得
把
代入②得，
所以方程组的解为
请用同样的方法解方程组：
. -
科目： 来源： 题型：
查看答案和解析>>【题目】某中学对七年级学生数学学期成绩的评价规定如下：学期评价得分由期中测试成绩(满分150分)和期末测试成绩(满分150分)两部分组成，其中期中测试成绩占30%，期末测试成绩占70%，当学期评价得分大于或等于130分时，该生数学学期成绩评价为优秀．（注：期中、期末成绩分数取整数）
(1)小明的期中成绩和期末测试成绩两项得分之和为260分，学期评价得分为132分，则小明期中测试成绩和期末测试成绩各得多少分？
(2)某同学期末测试成绩为120分，他的综合评价得分有可能达到优秀吗？为什么？
(3)如果一个同学学期评价得分要达到优秀，他的期末测试成绩至少要多少分（结果保留整数）？
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，四边形OABC为矩形，OA在x轴正半轴上，OC在y轴正半轴上，且A（10，0）、C（0，8）
（1）如图1，在矩形OABC的边AB上取一点E，连接OE，将△AOE沿OE折叠，使点A恰好落在BC边上的F处，求AE的长；
（2）将矩形OABC的AB边沿x轴负方向平移至MN（其它边保持不变），M、N分别在边OA、CB上且满足CN＝OM＝OC＝MN．如图2，P、Q分别为OM、MN上一点．若∠PCQ＝45°，求证：PQ＝OP+NQ；
（3）如图3，S、G、R、H分别为OC、OM、MN、NC上一点，SR、HG交于点D．若∠SDG＝135°，HG＝4
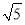，求RS的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】2017年3月全国两会胜利召开，某学校就两会期间出现频率最高的热词：A．蓝天保卫战，B．不动产保护，C．经济增速，D．简政放权等进行了抽样调查，每个同学只能从中选择一个“我最关注”的热词，如图是根据调查结果绘制的两幅不完整的统计图．请你根据统计图提供的信息，解答下列问题：
（1）本次调查中，一共调查了 名同学；
（2）条形统计图中，m= ，n= ；
（3）从该校学生中随机抽取一个最关注热词D的学生的概率是多少？
【答案】（1）300；（2）60，90；（3）从该校学生中随机抽取一个最关注热词D的学生的概率是
．【解析】试题分析：（1）根据A的人数为105人，所占的百分比为35%，求出总人数，即可解答；
（2）C所对应的人数为：总人数×30%，B所对应的人数为：总人数﹣A所对应的人数﹣C所对应的人数﹣D所对应的人数，即可解答；
（3）根据概率公式，即可解答．
试题解析：（1）105÷35%=300（人），
故答案为：300；
（2）n=300×30%=90（人），
m=300﹣105﹣90﹣45=60（人）．
故答案为：60，90；
（3）从该校学生中随机抽取一个最关注热词D的学生的概率是
=
，答：从该校学生中随机抽取一个最关注热词D的学生的概率是
．【题型】解答题
【结束】
26【题目】已知正方形ABCD的边长为8，点E为BC的中点，连接AE，并延长交射线DC于点F，将△ABE沿着直线AE翻折，点B落在B′处，延长AB′，交直线CD于点M．
（1）判断△AMF的形状并证明；
（2）将正方形变为矩形ABCD，且AB=6，BC=8，若B′恰好落在对角线AC上时，得到图2，此时CF=_____，
=_____；（3）在（2）的条件下，点E在BC边上．设BE为x，△ABE沿直线AE翻折后与矩形ABCD重合的面积为y，求y与x之间的函数关系式．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，在
的正方形网格中，从点
出发的四条线段
，
，
，
，它的另一个端点
，
，
，
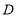均在格点上（正方形网格的交点）．
（1）若每个小正方形的边长都是1，分别求出
，，，的长度（结果保留根号）．（2）在
，，，四条线段中，是否存在三条线段，它们能构成直角三角形？如果存在，请指出是哪三条线段，并说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，已知
，
，
三点，其中a=
，b，c满足关系式
，P是第二象限内一点，连接PO，且P、A、C三点在一条直线上.（1）求A、B、C三点的坐标;
（2）若规定：在三角形中，若两条边相等，则这两条边与第三边的夹角相等。如在△DEF中，DE=DF，则∠E＝∠F.在本图中若PA=PO,AB=AC,CB⊥OB，垂足为B.求证：AB∥PO.
（3）如果在第二象限内有一点P(-2，
)，求四边形POBC的面积.
相关试题
