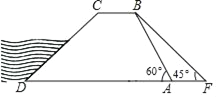
【题目】如图,水坝的横断面是梯形,背水坡AB的坡角∠BAD=60°,坡长AB=20![]() m,为加强水坝强度,将坝底从A处向后水平延伸到F处,使新的背水坡的坡角∠F=45°,求AF的长度.
m,为加强水坝强度,将坝底从A处向后水平延伸到F处,使新的背水坡的坡角∠F=45°,求AF的长度.
参考答案:
【答案】AF的长约为(30-10![]() )米.
)米.
【解析】试题分析:过B作DF的垂线,设垂足为E;可在Rt△ABE中,根据坡面AB的长以及坡角的度数,求得铅直高度BE和水平宽AE的值,进而可在Rt△BFE中,根据BE的长及坡角的度数,通过解直角三角形求出EF的长;根据AF=EF-AE,即可得出AF的长度.
试题解析:过B作BE⊥DF于E.

Rt△ABE中,AB=20![]() m,∠BAE=60°,
m,∠BAE=60°,
∴BE=ABsin60°=20![]() ×
×![]() =30,
=30,
AE=ABcos60°=20![]() ×
×![]() =10
=10![]() .
.
Rt△BEF中,BE=30,∠F=45°,
∴EF=BE=30.
∴AF=EF﹣AE=30﹣10![]() ,
,
即AF的长约为(30﹣10![]() )米.
)米.
-
科目: 来源: 题型:
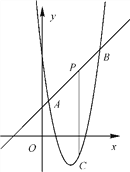
查看答案和解析>>【题目】如图,直线y=x+2与抛物线y=ax2+bx+6相交于A(
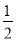 ,
, 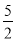 )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴,交抛物线于点C.
)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴,交抛物线于点C.(1)求抛物线的表达式;
(2)是否存在这样的点P,使线段PC的长有最大值?若存在,求出这个最大值,若不存在,请说明理由;
(3)当△PAC为直角三角形时,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在Rt△ABC,∠ACB=90°,分别以AB、BC为一边向外作正方形ABFG、BCED,连结AD、CF,AD与CF交于点M.

(1)求证:△ABD≌△FBC;
(2)如图(2),求证:AM2+MF2=AF2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小丽准备测一根旗杆AB的高度,已知小丽的眼睛离地面的距离EC=1.5米,第一次测量点C和第二次测量点D之间的距离CD=10米,∠AEG=30°,∠AFG=60°,请你帮小丽计算出这根旗杆的高度.(结果保留根号)
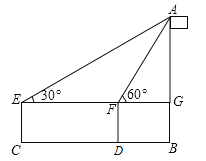
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有个形如六边形的点阵,它的中心是一个点,算第一层,第二层每边有两个点,第三层每边有三个点,依此类推.
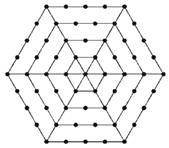
(1)填写下表:
层数
1
2
3
4
5
6
该层对应的点数
1
6
_____
18
_____
_____
(2)写出第n层所对应的点数为_____;
(3)如果某一层共96个点,那么它是第_____层,此时所有层中共有_____个点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,要在平行四边形
 内作一个菱形.甲,乙两位同学的作法分别如下:
内作一个菱形.甲,乙两位同学的作法分别如下:
对于甲乙两人的作法,可判断( )
A.甲正确,乙错误B.甲错误,乙正确C.甲,乙均正确D.甲、乙均错误
-
科目: 来源: 题型:
查看答案和解析>>【题目】某实验学校为了解九年级学生的身体素质测试情况,随机抽取了该校九年级部分学生的身体素质测试成绩作为样本,按
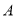 (优秀),
(优秀),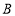 (良好),
(良好),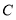 (合格),
(合格),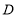 (不合格)四个等级进行统计,并将统计结果绘制了下面两幅不完整的统计图,请根据图中提供的信息,解答下列问题:
(不合格)四个等级进行统计,并将统计结果绘制了下面两幅不完整的统计图,请根据图中提供的信息,解答下列问题: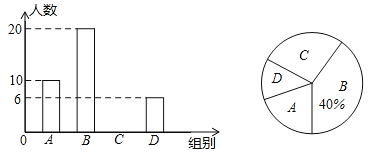
(1)此次共调查了多少名学生?
(2)将条形统计图补充完整,并计算扇形统计图中“
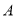 ”部分所对应的圆心角的度数为________°.
”部分所对应的圆心角的度数为________°.(3)我校九年级共有
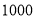 名学生参加了身体素质测试,估计测试成绩在良好以上(含良好)的人数.
名学生参加了身体素质测试,估计测试成绩在良好以上(含良好)的人数.
相关试题

