【题目】如图1,在平面直角坐标系中,点A坐标为(2,0),点B在x轴负半轴上,C在y轴正半轴上,∠ACB=90°,∠ABC=30°.
(1)求点B坐标;
(2)如图2,点P从B出发,沿线段BC运动,点P运动速度为每秒2个单位长度,设运动时间为t秒,用含t的式子表示三角形△OBP的面积S;
(3)如图3,在(2)的条件下,点P出发的同时,点Q从O出发,在线段OC上运动,运动速度为每秒2个单位长度,一个点到达终点,另一个点也停止运动.连接PQ,以PQ为一边,在第二象限作等边△PQM,作ME⊥y轴于E,点D为PC中点,作DN⊥BC交y轴于N,若CE=BP,BC=4![]() ,求N的坐标.
,求N的坐标.

参考答案:
【答案】(1)B(﹣6,0);(2)S=3t;(3)N(0,﹣![]() ).
).
【解析】
(1) 由A(2,0),可得OA=2,根据含30°角的直角三角形的性质求出AC 、AB即可解决问题;
(2)如图1,作高线PG,根据直角三角形30度角的性质可得PG的长为t,利用三角形面积公式可得S;
(3)如图2,作辅助线,证明△PCN是等边三角形,再证明△MPC≌△QPN(SAS),得QN=CM,∠MCP=∠QNP=60°,得到30度的直角△MCE,并求得CM=QN=2![]() ,根据CE=BP可得结论.
,根据CE=BP可得结论.
解:(1)∵A(2,0),
∴OA=2,
∵∠ACB=90°,∠ABC=30°,
∴∠BAC=60°,
∴∠ACO=30°,
∴AC=2OA=4,
∴AB=2AC=8,
∴OB=8﹣2=6,
∴B(﹣6,0).
(2)如图1,过P作PG⊥x轴于G,
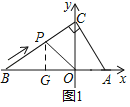
由题意得:BP=2t,
Rt△BPG中,∠B=30°,
∴PG=![]() BP=t,
BP=t,
∴S=![]() =
=![]() ×6×t=3t;
×6×t=3t;
(3)如图2,连接PN、CM.
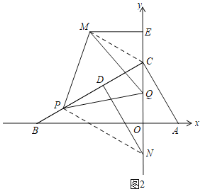
∵BP=2t,BC=4![]() ,
,
∴PC=4![]() ﹣2t,
﹣2t,
∵D是PC的中点,
∴PD=CD,
∵DN⊥PC,
∴PN=CN,
∵∠PCN=60°,
∴△PCN是等边三角形,
∴PC=PN=CN=4![]() ﹣2t,∠NPC=60°,
﹣2t,∠NPC=60°,
∵△PQM是等边三角形,
∴PM=PQ,∠MPQ=60°,
∴∠MPQ=∠CPN=60°,
∴∠MPC=∠QPN,
∴△MPC≌△QPN(SAS),
∴QN=CM,∠MCP=∠QNP=60°,
∵∠PCN=60°,
∴∠MCE=60°,
∵OC=2![]() ,OQ=2t,
,OQ=2t,
∴CQ=2![]() ﹣2t,
﹣2t,
∴QN=CN﹣CQ=4![]() ﹣2t﹣(2
﹣2t﹣(2![]() ﹣2t)=2
﹣2t)=2![]() ,
,
∴CM=QN=2![]() ,
,
Rt△MCE中,∠MCE=60°,
∴CE=![]() CM=
CM=![]() ,
,
∵CE=BP=2t=![]() ,
,
∴ON=QN﹣OQ=2![]() ﹣2t=2
﹣2t=2![]() ﹣
﹣![]() =
=![]() ,
,
∴N(0,﹣![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为
 (m2),种草所需费用
(m2),种草所需费用 1(元)与
1(元)与 (m2)的函数关系式为
(m2)的函数关系式为 ,其图象如图所示:栽花所需费用
,其图象如图所示:栽花所需费用 2(元)与x(m2)的函数关系式为
2(元)与x(m2)的函数关系式为 2=﹣0.01
2=﹣0.01 2﹣20
2﹣20 +30000(0≤
+30000(0≤ ≤1000).
≤1000).
(1)请直接写出k1、k2和b的值;
(2)设这块1000m2空地的绿化总费用为W(元),请利用W与
 的函数关系式,求出绿化总费用W的最大值;
的函数关系式,求出绿化总费用W的最大值;(3)若种草部分的面积不少于700m2,栽花部分的面积不少于100m2,请求出绿化总费用W的最小值.
-
科目: 来源: 题型:
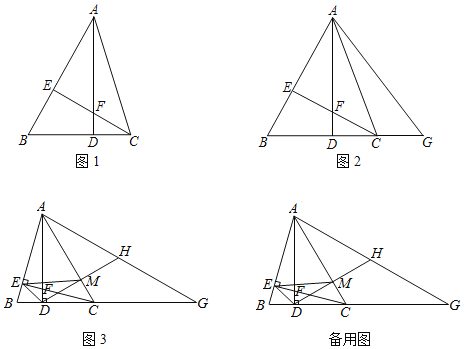
查看答案和解析>>【题目】如图1,在△ABC中,AD⊥BC于D,CE⊥AB于E,AD与CE交于点F,∠ACE=45°.
(1)求证:BE=EF;
(2)如图2,G在BC的延长线上,连接GA,若GA=GB,求证:AC平分∠DAG;
(3)如图3,在(2)的条件下,H为AG的中点,连接DH交AC于M,连接EM、ED,若S△EMC=4,∠BAD=15°,求AM的长.
-
科目: 来源: 题型:
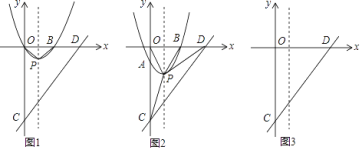
查看答案和解析>>【题目】如图,平面直角坐标系中,抛物线y=x2﹣2x与x轴交于O、B两点,顶点为P,连接OP、BP,直线y=x﹣4与y轴交于点C,与x轴交于点D.
(1)写出点B坐标;判断△OBP的形状;
(2)将抛物线沿对称轴平移m个单位长度,平移的过程中交y轴于点A,分别连接CP、DP;
(i)若抛物线向下平移m个单位长度,当S△PCD=
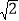 S△POC时,求平移后的抛物线的顶点坐标;
S△POC时,求平移后的抛物线的顶点坐标;(ii)在平移过程中,试探究S△PCD和S△POD之间的数量关系,直接写出它们之间的数量关系及对应的m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD平分
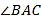 ,AB=AC,则此图中全等三角形有( )
,AB=AC,则此图中全等三角形有( )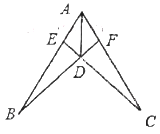
A.2对B.3对C.4对D.5对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=20°,点P在OA边上.
(1)以点O为圆心,OP长为半径作
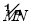 ,交OB于点C;
,交OB于点C;(2)分别以点P、C为圆心,PC长为半径作弧,交
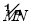 于点D、E;
于点D、E;(3)连接DE,分别交OC、OP于点F、G;
(4)连接DP.
根据以上作图过程及所作图形,下列结中正确的是_____.(填序号)
①OC垂直平分DP;②∠COD=∠COP;③DF=FG;④OD=DE.
-
科目: 来源: 题型:
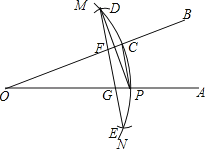
查看答案和解析>>【题目】对角线长分别为6和8的菱形ABCD如图所示,点O为对角线的交点,过点O折叠菱形,使B,B′两点重合,MN是折痕.若B'M=1,则CN的长为( )
A. 7 B. 6 C. 5 D. 4
相关试题

