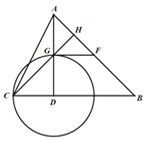
【题目】如图,在△ABC中,∠B=45°,AD⊥BC于点D,以D为圆心DC为半径作⊙D交AD于点G,过点G作⊙D的切线交AB于点F,且F恰好为AB中点.
(1)求tan∠ACD的值.
(2)连结CG并延长交AB于点H,若AH=2,求AC的长.
参考答案:
【答案】(1)2;(2)![]()
【解析】解:(1)∵FG与⊙D相切 ∴∠DGF=90°∵AD⊥BC
∴FG∥CB∵F为AB中点∴ ![]()
∴AD=2GD=2CD∴tan∠ACD=2
(2)∵AD⊥BC∴∠ADB=90° ∵∠B=45°∴△ADB是等腰直角三角形∴∠DAB=45°
∵GD=CD,∠GDC=90°∴△CGD是等腰直角三角形∴∠GCD=45°
∴∠AHC=90° ∴△AGH是等腰直角三角形∵AH=2,∴HG=2,![]()
∴GD=![]() ∴CG=4∴HC=6∴
∴CG=4∴HC=6∴![]()

-
科目: 来源: 题型:
查看答案和解析>>【题目】某水资源保护组织对石家庄某小区的居民进行节约水资源的问卷调查.某居民在问卷上的选项代号画“√”,这个过程是收集数据中的( )
A.确定调查范围
B.汇总调查数据
C.实施调查
D.明确调查问题 -
科目: 来源: 题型:
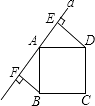
查看答案和解析>>【题目】如图所示,直线a经过正方形ABCD的顶点A,分别过顶点B、D作DE⊥a于点E、BF⊥a于点F,若DE=4,BF=3,则EF的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果抛物线y=(1﹣a)x2+1的开口向下,那么a的取值范围是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】腰长为x,底边长为y的等腰三角形的周长为12,则y与x的函数表达式为____________,自变量x的取值范围为____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,一个点的横、纵坐标都是整数,并且它们的乘积是4,满足这条件的点共有______个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,AB=3,BC=4,将△ABC折叠,使点B恰好落在边AC上,与点B′重合,AE为折痕,则EB′= .

相关试题

