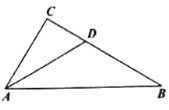
【题目】如图,∠CAB+∠ABC=90°,AD平分∠CAB,与BC边交于点D,BE平分∠ABC与AC边交于点E。
(1)依题意补全图形,并猜想∠DAB+∠EBA的度数等于__________;
(2)证明以上结论。
证明:∵ AD平分∠CAB,BE平分∠ABC,
∴∠DAB=![]() ∠CAB,
∠CAB,
∠EBA=__________.
(理由:____________________)
∵∠CAB+∠ABC=90°,
∴∠DAB+∠EBA=______×(∠______+∠______)=______。
参考答案:
【答案】图像见详解;45![]()
![]() ∠CBA; 角平方线的定义
∠CBA; 角平方线的定义 ![]() CAB ABC 45°
CAB ABC 45°
【解析】
(1)根据题意画出图形,然后由角平分线的定义可求得∠DAB+∠EBA =45![]() ;
;
(2)根据角平分线的定义以及证明过程进行填写即可.
(1)解:如图所示: 
猜想∠DAB+∠EBA =45![]() .
.
(2)证明: 证明:∵ AD平分∠CAB,BE平分∠ABC,
∴∠DAB=![]() ∠CAB,
∠CAB,
∠EBA=![]() ∠CBA.
∠CBA.
(理由:角平方线的定义)
∵∠CAB+∠ABC=90°,
∴∠DAB+∠EBA=![]() ×(∠CAB +∠ABC)=45°.
×(∠CAB +∠ABC)=45°.
故答案:![]() ∠CAB;角平方线的定义;
∠CAB;角平方线的定义;![]() ;CAB ;ABC;45°.
;CAB ;ABC;45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,有如图所示的Rt△ABO,AB⊥x轴于点B,斜边AO=10,sin∠AOB=
 ,反比例函数
,反比例函数  的图象经过AO的中点C,且与AB交于点D,则点D的坐标为 .
的图象经过AO的中点C,且与AB交于点D,则点D的坐标为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中小方格边长为1,请你根据所学的知识解决下面问题.
(1)求网格图中△ABC的面积.
(2)判断△ABC是什么形状?并所明理由.

-
科目: 来源: 题型:
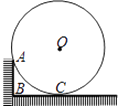
查看答案和解析>>【题目】木工师傅可以用角尺测量并计算出圆的半径r,用角尺的较短边紧靠⊙O,并使较长边与⊙O相切于点C,假设角尺的较长边足够长,角尺的顶点为B,较短边AB=8cm,若读得BC长为acm,则用含a的代数式表示r为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式
 ,并把解在数轴上表示出来.
,并把解在数轴上表示出来. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】有足够多的长方形和正方形卡片,如下图:
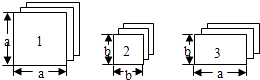
(1)如果选取1号、2号、3号卡片分别为1张、2张、3张,可拼成一个长方形(不重叠无缝隙),请画出这个长方形的草图,并运用拼图前后面积之间的关系说明这个长方形的代数意义.
这个长方形的代数意义是 .
(2)小明想用类似方法解释多项式乘法(a+3b)(2a+b)=2a2+7ab+3b2 , 那么需用2号卡片张,3号卡片张. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校初一年级两个班的学生要到航天科普教育基地进行社会大课堂活动,两班学生共104人,其中初一(1)班有40多人,不足50人,教育基地门票价格如下:
购票张数
1~50张
51~100张
100张以上
每张票的价格
12元
10元
8元
原计划两班都以班为单位购票,则一共应付1240元,请回答下列问题:
(1)初一(1)班有多少人?
(2)你作为组织者如何购票最省钱?比原计划省多少钱?
相关试题

