【题目】木工师傅可以用角尺测量并计算出圆的半径r,用角尺的较短边紧靠⊙O,并使较长边与⊙O相切于点C,假设角尺的较长边足够长,角尺的顶点为B,较短边AB=8cm,若读得BC长为acm,则用含a的代数式表示r为 . 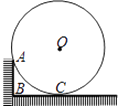
参考答案:
【答案】r=8时,r=a;当r>8时, ![]()
【解析】解:①如图所示, 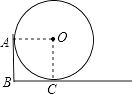
r≤8时,
∵OA⊥BA,OC⊥BC,∠B=90°,
∴四边形OABC是矩形,
∴BC=AO,
∴r=a;
②当r>8时,
如图:连接OC,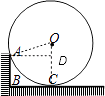
∵BC与⊙O相切于点C,
∴OC⊥BC,
连接OA,过点A作AD⊥OC于点D,
则四边形ABCD是矩形,即AD=BC,CD=AB.
在Rt△AOD中,OA2=OD2+AD2 ,
即:r2=(r﹣8)2+a2 ,
整理得:r= ![]() a2+4.
a2+4.
故答案是:r=8时,r=a;当r>8时, ![]() .
.
【考点精析】掌握勾股定理的概念和切线的性质定理是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合探究题 等腰三角形ABC中,AB=x,BC=y,周长为12.
(1)列出关于x,y的二元一次方程;
(2)求该方程的所有整数解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,有如图所示的Rt△ABO,AB⊥x轴于点B,斜边AO=10,sin∠AOB=
 ,反比例函数
,反比例函数  的图象经过AO的中点C,且与AB交于点D,则点D的坐标为 .
的图象经过AO的中点C,且与AB交于点D,则点D的坐标为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中小方格边长为1,请你根据所学的知识解决下面问题.
(1)求网格图中△ABC的面积.
(2)判断△ABC是什么形状?并所明理由.

-
科目: 来源: 题型:
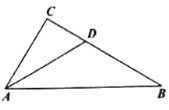
查看答案和解析>>【题目】如图,∠CAB+∠ABC=90°,AD平分∠CAB,与BC边交于点D,BE平分∠ABC与AC边交于点E。
(1)依题意补全图形,并猜想∠DAB+∠EBA的度数等于__________;
(2)证明以上结论。
证明:∵ AD平分∠CAB,BE平分∠ABC,
∴∠DAB=
 ∠CAB,
∠CAB,∠EBA=__________.
(理由:____________________)
∵∠CAB+∠ABC=90°,
∴∠DAB+∠EBA=______×(∠______+∠______)=______。
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式
 ,并把解在数轴上表示出来.
,并把解在数轴上表示出来. 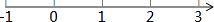
-
科目: 来源: 题型:
查看答案和解析>>【题目】有足够多的长方形和正方形卡片,如下图:
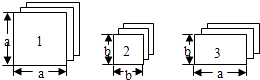
(1)如果选取1号、2号、3号卡片分别为1张、2张、3张,可拼成一个长方形(不重叠无缝隙),请画出这个长方形的草图,并运用拼图前后面积之间的关系说明这个长方形的代数意义.
这个长方形的代数意义是 .
(2)小明想用类似方法解释多项式乘法(a+3b)(2a+b)=2a2+7ab+3b2 , 那么需用2号卡片张,3号卡片张.
相关试题

