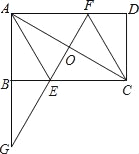
【题目】如图,在矩形ABCD中,点O是AC的中点,AC=2AB,延长AB至G,使BG=AB,连接GO交BC于E,延长GO交AD于F,连接AE.
求证:(1)△ABC≌△AOG;
(2)猜测四边形AECF的形状并证明你的猜想.
参考答案:
【答案】(1)证明见解析;(2)四边形AECF是菱形;理由见解析
【解析】
(1)由已知条件得出AB=AO,AC=AG,由SAS证明△ABC≌△AOG即可;
(2)由矩形的性质得出∠ABC=90°,AD∥BC,得出∠OAF=∠OCE,由ASA证明△AOF≌△COE,得出OF=OE,得出四边形AECF是平行四边形,再由全等三角形的对应角相等得出∠AOG=∠ABC=90°,即可得出结论.
(1)证明:∵点O是AC的中点,
∴AO=CO=![]() AC,
AC,
∵AC=2AB,BG=AB,
∴AB=AO,AC=AG,
在△ABC和△AOG中,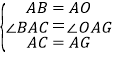 ,
,
∴△ABC≌△AOG(SAS);
(2)四边形AECF是菱形;理由如下:
∵四边形ABCD是矩形,
∴∠ABC=90°,AD∥BC,
∴∠OAF=∠OCE,
在△AOF和△COE中,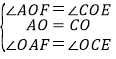 ,
,
∴△AOF≌△COE(ASA),
∴OF=OE,
∴四边形AECF是平行四边形,
∵△ABC≌△AOG,
∴∠AOG=∠ABC=90°,
∴AC⊥EF,
∴四边形AECF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明从家里骑自行车到学校,每小时骑20km,可早到
 小时,每小时骑15km就会迟到
小时,每小时骑15km就会迟到 小时,问他家到学校的路程是多少km?
小时,问他家到学校的路程是多少km? -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车间同时开始加工一批服装.从开始加工到加工完这批服装甲车间工作了9小时,乙车间在中途停工一段时间维修设备,然后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止.设甲、乙两车间各自加工服装的数量为y(件).甲车间加工的时间为x(时),y与x之间的函数图象如图所示.
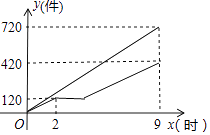
(1)甲车间每小时加工服装件数为件;这批服装的总件数为件.
(2)求乙车间维修设备后,乙车间加工服装数量y与x之间的函数关系式;
(3)求甲、乙两车间共同加工完1000件服装时甲车间所用的时间. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与CD相交于O,OE⊥AB,OF⊥CD.
(1)图中与∠AOF互余的角是______,与∠COE互补的角是______;(把符合条件的角都写出来)
(2)如果∠AOC=
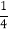 ∠EOF,求∠EOF的度数.
∠EOF,求∠EOF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题【再现】如图①,在△ABC中,点D,E分别是AB,AC的中点,可以得到:DE∥BC,且DE=
 BC.(不需要证明)
BC.(不需要证明)
(1)【探究】如图②,在四边形ABCD中,点E,F,G,H分别是AB,BC,CD,DA的中点,判断四边形EFGH的形状,并加以证明.
(2)【应用】在(1)【探究】的条件下,四边形ABCD中,满足什么条件时,四边形EFGH是菱形?你添加的条件是: . (只添加一个条件)
(3)如图③,在四边形ABCD中,点E,F,G,H分别是AB,BC,CD,DA的中点,对角线AC,BD相交于点O.若AO=OC,四边形ABCD面积为5,则阴影部分图形的面积和为 .
-
科目: 来源: 题型:
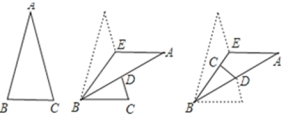
查看答案和解析>>【题目】如图,△ABC中∠A=30°,E是AC边上的点,先将△ABE沿着BE翻折,翻折后△ABE的AB边交AC于点D,又将△BCD沿着BD翻折,C点恰好落在BE上,此时∠CDB=80°,则原三角形的∠B为 _____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在Rt△ABC中,∠C=90°,AB=10,BC=6,点P从点A出发,沿折线AB﹣BC向终点C运动,在AB上以每秒5个单位长度的速度运动,在BC上以每秒3个单位长度的速度运动,点Q从点C出发,沿CA方向以每秒
 个单位长度的速度运动,P,Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.
个单位长度的速度运动,P,Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.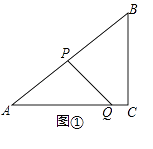
(1)求线段AQ的长;(用含t的代数式表示)
(2)连结PQ,当PQ与△ABC的一边平行时,求t的值;
(3)如图②,过点P作PE⊥AC于点E,以PE,EQ为邻边作矩形PEQF,点D为AC的中点,连结DF.设矩形PEQF与△ABC重叠部分图形的面积为S.①当点Q在线段CD上运动时,求S与t之间的函数关系式;②直接写出DF将矩形PEQF分成两部分的面积比为1:2时t的值.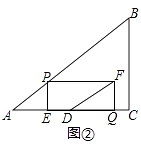
相关试题

