【题目】如图①,在Rt△ABC中,∠C=90°,AB=10,BC=6,点P从点A出发,沿折线AB﹣BC向终点C运动,在AB上以每秒5个单位长度的速度运动,在BC上以每秒3个单位长度的速度运动,点Q从点C出发,沿CA方向以每秒 ![]() 个单位长度的速度运动,P,Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.
个单位长度的速度运动,P,Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.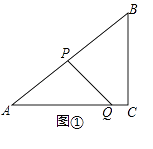
(1)求线段AQ的长;(用含t的代数式表示)
(2)连结PQ,当PQ与△ABC的一边平行时,求t的值;
(3)如图②,过点P作PE⊥AC于点E,以PE,EQ为邻边作矩形PEQF,点D为AC的中点,连结DF.设矩形PEQF与△ABC重叠部分图形的面积为S.①当点Q在线段CD上运动时,求S与t之间的函数关系式;②直接写出DF将矩形PEQF分成两部分的面积比为1:2时t的值.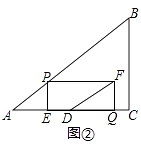
参考答案:
【答案】
(1)解:在Rt△ABC中,∵∠C=90°,AB=10,BC=6,
∴AC= ![]() =
= ![]() =8,
=8,
∵CQ= ![]() t,
t,
∴AQ=8﹣ ![]() t(0≤t≤4).
t(0≤t≤4).
(2)解:①当PQ∥BC时, ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴t= ![]() s.
s.
②当PQ∥AB时, ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴t=3,
综上所述,t= ![]() s或3s时,当PQ与△ABC的一边平行.
s或3s时,当PQ与△ABC的一边平行.
(3)解:①如图1中,a、当0≤t≤ ![]() 时,重叠部分是四边形PEQF.
时,重叠部分是四边形PEQF.
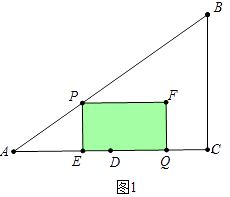
S=PEEQ=3t(8﹣4t﹣ ![]() t)=﹣16t2+24t.
t)=﹣16t2+24t.
b、如图2中,当 ![]() <t≤2时,重叠部分是四边形PNQE.
<t≤2时,重叠部分是四边形PNQE.
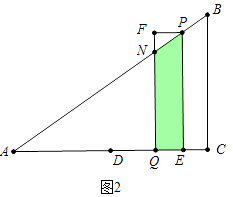
S=S四边形PEQF﹣S△PFN=(16t2﹣24t)﹣ ![]()
![]() [5t﹣
[5t﹣ ![]() (8﹣
(8﹣ ![]() t)]
t)] ![]() [5t﹣
[5t﹣ ![]()
![]() t)]=
t)]= ![]() .
.
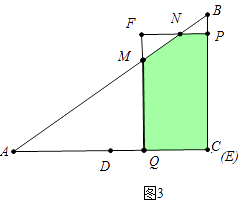
c、如图3中,当2<t≤3时,重叠部分是五边形MNPBQ.
S=S四边形PBQF﹣S△FNM= ![]() t[6﹣3(t﹣2)]﹣
t[6﹣3(t﹣2)]﹣ ![]() [
[ ![]() t﹣4(t﹣2)]
t﹣4(t﹣2)] ![]() [
[ ![]() t﹣4(t﹣2)]=﹣
t﹣4(t﹣2)]=﹣ ![]() t2+32t﹣24.
t2+32t﹣24.
②a、如图4中,当DE:DQ=1:2时,DF将矩形PEQF分成两部分的面积比为1:2.
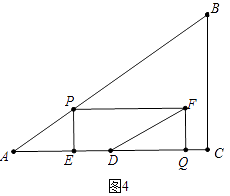
则有(4﹣4t):(4﹣ ![]() t)=1:2,解得t=
t)=1:2,解得t= ![]() s,
s,
b、如图5中,当NE:PN=1:2时,DF将矩形PEQF分成两部分的面积比为1:2.
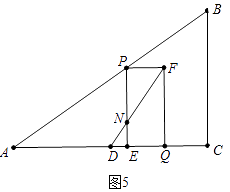
∴DE:DQ=NE:FQ=1:3,
∴(4t﹣4):(4﹣ ![]() t)=1:3,
t)=1:3,
解得t= ![]() s,
s,
综上所述,当t= ![]() s或
s或 ![]() s时,DF将矩形PEQF分成两部分的面积比为1:2.
s时,DF将矩形PEQF分成两部分的面积比为1:2.
【解析】(1)由线段之差可表示出AQ=8﹣ ![]() t;(2)由于点Q在AC上,PQ不会与AC平行,因此分类讨论PQ∥BC与PQ∥AB两类;(2)以t=2和
t;(2)由于点Q在AC上,PQ不会与AC平行,因此分类讨论PQ∥BC与PQ∥AB两类;(2)以t=2和![]() 为分界点分为三段:0≤t≤
为分界点分为三段:0≤t≤ ![]() 、
、 ![]() <t≤2、2<t≤3;(3)需分类为两种:左上:右下=1:2和左上:右下=2:1.
<t≤2、2<t≤3;(3)需分类为两种:左上:右下=1:2和左上:右下=2:1.
【考点精析】关于本题考查的函数关系式,需要了解用来表示函数关系的数学式子叫做函数解析式或函数关系式才能得出正确答案.
-
科目: 来源: 题型:
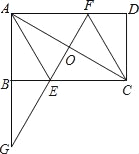
查看答案和解析>>【题目】如图,在矩形ABCD中,点O是AC的中点,AC=2AB,延长AB至G,使BG=AB,连接GO交BC于E,延长GO交AD于F,连接AE.
求证:(1)△ABC≌△AOG;
(2)猜测四边形AECF的形状并证明你的猜想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题【再现】如图①,在△ABC中,点D,E分别是AB,AC的中点,可以得到:DE∥BC,且DE=
 BC.(不需要证明)
BC.(不需要证明)
(1)【探究】如图②,在四边形ABCD中,点E,F,G,H分别是AB,BC,CD,DA的中点,判断四边形EFGH的形状,并加以证明.
(2)【应用】在(1)【探究】的条件下,四边形ABCD中,满足什么条件时,四边形EFGH是菱形?你添加的条件是: . (只添加一个条件)
(3)如图③,在四边形ABCD中,点E,F,G,H分别是AB,BC,CD,DA的中点,对角线AC,BD相交于点O.若AO=OC,四边形ABCD面积为5,则阴影部分图形的面积和为 .
-
科目: 来源: 题型:
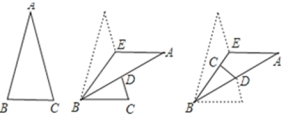
查看答案和解析>>【题目】如图,△ABC中∠A=30°,E是AC边上的点,先将△ABE沿着BE翻折,翻折后△ABE的AB边交AC于点D,又将△BCD沿着BD翻折,C点恰好落在BE上,此时∠CDB=80°,则原三角形的∠B为 _____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,D是BC的中点,且AD=AC,DE⊥BC,与AB相交于点E,EC与AD相交于点F.

(1)求证:△ABC∽△FCD;
(2)若DE=3,BC=8,求△FCD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
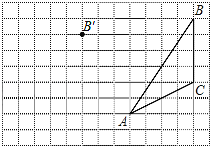
(1)在给定方格纸中画出平移后的△A′B′C′;
(2)画出AB边上的中线CD和BC边上的高线AE;
(3)线段AA′与线段BB′的关系是: ;
(4)求△A′B′C′的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )

A. BD=CE B. AD=AE C. DA=DE D. BE=CD
相关试题

