搜索
【题目】小明从家里骑自行车到学校，每小时骑20km，可早到
小时，每小时骑15km就会迟到
小时，问他家到学校的路程是多少km？
参考答案：
【答案】他家到学校的路程是25km．
【解析】
方法一：设小明他家到学校的路程为xkm．根据“每小时骑20km所用的时间+
=每小时骑15km所用的时间-
”列出方程，求解即可；
方法二：设小明到学校的时间为x小时．根据路程不变列出方程，并解答．
解：方法一：设小明他家到学校的路程为xkm，
依题意得：
+=
-，
解得x =25．
答：他家到学校的路程是25km；
方法二：设小明到学校的时间为x小时，
20（x-）=15（x+），
解得x =1.5．
他家到学校的路程为20×（1.5-）=25（千米）．
答：他家到学校的路程是25km．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点C在线段AB上，点M、N分别是AC、BC的中点．
（1）若AC=8cm，CB=6cm，求线段MN的长；
（2）若C为线段AB上任一点，满足AC+CB=a，其它条件不变，你能猜想MN的长度吗？写出你的结论并说明理由；
（3）若点C在线段AB的延长线上，且满足AC-BC=b，M、N分别为AC、BC的中点，你能猜想MN的长度吗？请画出图形并写出你的结论（不必说明理由）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】用适当的不等式表示下列不等关系：
（1）x减去6大于12；
（2）x的2倍与5的差是负数；
（3）x的3倍与4的和是非负数；
（4）y的5倍与9的差不大于
； -
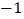科目： 来源： 题型：
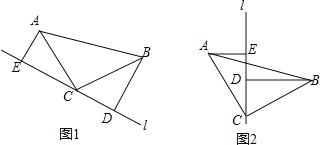
查看答案和解析>>【题目】如图，△ABC中，∠ACB=90°，AC=BC，直线l过点C，BD⊥l，AE⊥l，垂足分别为D、E．
（1）当直线l不与底边AB相交时，求证：ED=AE+BD；
（2）如图2，将直线l绕点C顺时针旋转，使l与底边AB相交时，请你探究ED、AE、BD三者之间的数量关系．
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两车间同时开始加工一批服装．从开始加工到加工完这批服装甲车间工作了9小时，乙车间在中途停工一段时间维修设备，然后按停工前的工作效率继续加工，直到与甲车间同时完成这批服装的加工任务为止．设甲、乙两车间各自加工服装的数量为y（件）．甲车间加工的时间为x（时），y与x之间的函数图象如图所示．
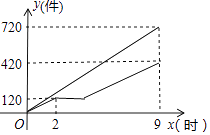
（1）甲车间每小时加工服装件数为件；这批服装的总件数为件．
（2）求乙车间维修设备后，乙车间加工服装数量y与x之间的函数关系式；
（3）求甲、乙两车间共同加工完1000件服装时甲车间所用的时间． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线AB与CD相交于O，OE⊥AB，OF⊥CD．
（1）图中与∠AOF互余的角是______，与∠COE互补的角是______；（把符合条件的角都写出来）
（2）如果∠AOC=
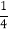∠EOF，求∠EOF的度数．
-
科目： 来源： 题型：
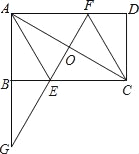
查看答案和解析>>【题目】如图，在矩形ABCD中，点O是AC的中点，AC＝2AB，延长AB至G，使BG＝AB，连接GO交BC于E，延长GO交AD于F，连接AE．
求证：（1）△ABC≌△AOG；
（2）猜测四边形AECF的形状并证明你的猜想．
相关试题
