【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与X轴交于点A、B两点B处的坐标为(3,0),与y轴交于c(0,﹣3),点P是直线BC下方抛物线上的动点.
(1)求出二次函数的解析式;
(2)连接PO、PC,并将△POC沿y轴对折,得到四边形POP′C,那么是否存在点P,使得四边形POP′C为菱形?若存在,求出点P的坐标,若存在,请说明理由;
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P的坐标和四边形ABPC的最大面积.
参考答案:
【答案】
(1)解:把B(3,0)、C(0,﹣3)代入y=x2+bx+c,得
![]() ,解得
,解得 ![]() ,
,
∴这个二次函数的表达式为y=x2﹣2x﹣3
(2)解:存在.理由如下:
如图1中,作OC的垂直平分线交直线BC下方的抛物线于点P,垂足为点E.

则PO=PC,
∵△POC沿CO翻折,得到四边形POP′C,
∴OP′=OP,CP′=CP,
∴OP′=OP=CP′=CP,
∴四边形POP′C为菱形,
∵C点坐标为(0,﹣3),
∴E点坐标为(0,﹣ ![]() ),
),
∴点P的纵坐标为﹣ ![]() ,
,
把y=﹣ ![]() 代入y=x2﹣2x﹣3得x2﹣2x﹣3=﹣
代入y=x2﹣2x﹣3得x2﹣2x﹣3=﹣ ![]() ,
,
解得x= ![]() ,
,
∵点P在直线BC下方的抛物线上,
∴x= ![]() ,
,
∴满足条件的点P的坐标为( ![]() ,﹣
,﹣ ![]() ).
).
(3)解:如图2中,作PF⊥x轴于F点,交BC于E点,BC的解析式为y=x﹣3,设E(m,m﹣3),P(m,m2﹣2m﹣3).
 ,
,
PE=m﹣3﹣(m2﹣2m﹣3)=﹣m2+3m=﹣(m﹣ ![]() )2+
)2+ ![]() ,
,
S△BCP=S△BEP+SCEP= ![]() PE×FB+
PE×FB+ ![]() EPOF
EPOF
= ![]() EPOB
EPOB
= ![]() ×3[﹣(m﹣
×3[﹣(m﹣ ![]() )2+
)2+ ![]() ]
]
=﹣ ![]() (m﹣
(m﹣ ![]() )2+
)2+ ![]() ,
,
∵﹣ ![]() <0,
<0,
∴当m= ![]() 时,S最大=
时,S最大= ![]() ,
,
此时P( ![]() ,﹣
,﹣ ![]() );
);
∵A(﹣1,0),B(3,0),C(0,﹣3),
∵四边形ACPB的面积=△ABC的面积+△PBC的面积,△ABC的面积= ![]() ×4×3=6=定值,
×4×3=6=定值,
∴当△PBC的面积最大时,四边形ACPB的面积最大,最大值为6+ ![]() =
= ![]()
【解析】1)将点B、C代入y=x2+bx+c可得到关于b、c的方程组,解方程组求即可。
(2)作OC的垂直平分线交直线BC下方的抛物线于点P,则PO=PC,根据翻折的性质得OP′=OP,CP′=CP,易证得四边形POP′C为菱形,就可以求得点E的坐标,将点P的纵坐标代入二次函数解析式,可求出对应x的值,根据点P在直线BC下方的抛物线上,然后确定满足条件的P点坐标。
(3)添加辅助线,作PF⊥x轴于F点,交BC于E点,BC的解析式为y=x-3,设E(m,m-3),P′(m,m2-2m-3).根据S△BCP=S△BEP+SCEP,构建s与m的二次函数,求出二次函数的顶点坐标,求出△PBC的面积的最大值,即可解决问题。
【考点精析】认真审题,首先需要了解确定一次函数的表达式(确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法),还要掌握二次函数的最值(如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在△
 中,
中,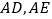 分别是△
分别是△ 的高和角平分线,若
的高和角平分线,若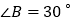 ,
,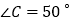 ;求
;求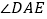 的度数.
的度数.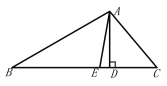
-
科目: 来源: 题型:
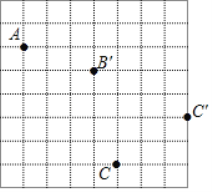
查看答案和解析>>【题目】画图并填空:如图,方格纸中每个小正方形的边长都为1,在方格纸中将△ABC经过一次平移后得到△A′B′C′,图中标出来点A,点B′、点C和它的对应点C′.
(1)请画出平移前后的△ABC和△A′B′C′;(注意并标注好字母)
(2)利用网格画出△ABC中BC边上的中线AD;(注意并标注好字母)
(3)利用网格画出△ABC中AB边上的高CE;(注意并标注好字母)
(4)△A′B′C′的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,延长AB至E,延长CD至F,BE=DF,连接EF,与BC、AD分别相交于P、Q两点.
(1)求证:CP=AQ;
(2)若BP=1,PQ=
 ,∠AEF=45°,求矩形ABCD的面积.
,∠AEF=45°,求矩形ABCD的面积.
-
科目: 来源: 题型:
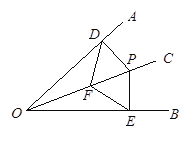
查看答案和解析>>【题目】如图,OC是∠AOB的角平分线,P是OC上一点.PD⊥OA交OA于D,PE⊥OB交OB于E,F是OC上的另一点,连接DF,EF.求证:DF=EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个大小不同的等腰直角三角形三角板如图
 所示放置,图
所示放置,图 是由它抽象出的几何图形,B,C,E在同一条直线上,联结DC,
是由它抽象出的几何图形,B,C,E在同一条直线上,联结DC, 请找出图
请找出图 中的全等三角形,并给予说明
中的全等三角形,并给予说明 说明:结论中不得含有未标识的字母
说明:结论中不得含有未标识的字母 ;
; 试说明:
试说明: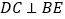 .
.
-
科目: 来源: 题型:
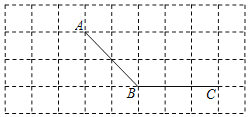
查看答案和解析>>【题目】如图,所有小正方形的边长都为1个单位,A、B、C均在格点上.
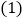 过点C画线段AB的平行线CD;
过点C画线段AB的平行线CD;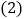 过点A画线段BC的垂线,垂足为E;
过点A画线段BC的垂线,垂足为E; 过点A画线段AB的垂线,交线段CB的延长线于点F;
过点A画线段AB的垂线,交线段CB的延长线于点F;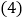 线段AE的长度是点______到直线______的距离;
线段AE的长度是点______到直线______的距离;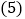 线段AE、BF、AF的大小关系是______
线段AE、BF、AF的大小关系是______ 用“
用“ ”连接
”连接
相关试题

