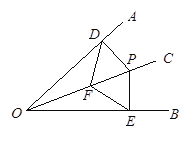
【题目】如图,OC是∠AOB的角平分线,P是OC上一点.PD⊥OA交OA于D,PE⊥OB交OB于E,F是OC上的另一点,连接DF,EF.求证:DF=EF.
参考答案:
【答案】证明见解析.
【解析】
试题证明线段相等的方法一般是三角形的全等,找到包含两条线段的两个三角形△DPF和△EPF,然后找全等的条件,角平分线线上的点到两边的距离相等,所以PD=PE,因为PE⊥OB,PD⊥AO,所以∠PDO=
∠PEO=90°,所以∠DPF=90°-∠DOP,∠EPF=90°-∠EOP,即∠DPF=∠EPF,在△DPF和△EPF中, PD="PE," ∠DPF=∠EPF,PF=PF,所以△DPF≌△EPF,所以DF=EF.
试题解析:∵点P在∠AOB的角平分线OC上,PE⊥OB,PD⊥AO,
∴PD=PE,∠DOP=∠EOP,∠PDO=∠PEO=90°,
∴∠DPF=90°-∠DOP,∠EPF=90°-∠EOP,
∴∠DPF=∠EPF,
在△DPF和△EPF中,
PD="PE," ∠DPF=∠EPF,PF=PF,
∴△DPF≌△EPF(ASA),
∴DF=EF.
-
科目: 来源: 题型:
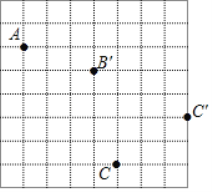
查看答案和解析>>【题目】画图并填空:如图,方格纸中每个小正方形的边长都为1,在方格纸中将△ABC经过一次平移后得到△A′B′C′,图中标出来点A,点B′、点C和它的对应点C′.
(1)请画出平移前后的△ABC和△A′B′C′;(注意并标注好字母)
(2)利用网格画出△ABC中BC边上的中线AD;(注意并标注好字母)
(3)利用网格画出△ABC中AB边上的高CE;(注意并标注好字母)
(4)△A′B′C′的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,延长AB至E,延长CD至F,BE=DF,连接EF,与BC、AD分别相交于P、Q两点.
(1)求证:CP=AQ;
(2)若BP=1,PQ=
 ,∠AEF=45°,求矩形ABCD的面积.
,∠AEF=45°,求矩形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与X轴交于点A、B两点B处的坐标为(3,0),与y轴交于c(0,﹣3),点P是直线BC下方抛物线上的动点.

(1)求出二次函数的解析式;
(2)连接PO、PC,并将△POC沿y轴对折,得到四边形POP′C,那么是否存在点P,使得四边形POP′C为菱形?若存在,求出点P的坐标,若存在,请说明理由;
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P的坐标和四边形ABPC的最大面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】两个大小不同的等腰直角三角形三角板如图
 所示放置,图
所示放置,图 是由它抽象出的几何图形,B,C,E在同一条直线上,联结DC,
是由它抽象出的几何图形,B,C,E在同一条直线上,联结DC, 请找出图
请找出图 中的全等三角形,并给予说明
中的全等三角形,并给予说明 说明:结论中不得含有未标识的字母
说明:结论中不得含有未标识的字母 ;
; 试说明:
试说明: .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,所有小正方形的边长都为1个单位,A、B、C均在格点上.
 过点C画线段AB的平行线CD;
过点C画线段AB的平行线CD;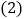 过点A画线段BC的垂线,垂足为E;
过点A画线段BC的垂线,垂足为E; 过点A画线段AB的垂线,交线段CB的延长线于点F;
过点A画线段AB的垂线,交线段CB的延长线于点F;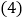 线段AE的长度是点______到直线______的距离;
线段AE的长度是点______到直线______的距离;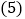 线段AE、BF、AF的大小关系是______
线段AE、BF、AF的大小关系是______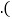 用“
用“ ”连接
”连接
-
科目: 来源: 题型:
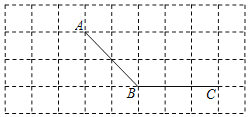
查看答案和解析>>【题目】如图,在距离铁轨200米的B处,观察由南宁开往百色的“和谐号”动车,当动车车头在A处时,恰好位于B处的北偏东60°方向上;10秒钟后,动车车头到达C处,恰好位于B处的西北方向上,则这时段动车的平均速度是( )米/秒.

A.20( +1)
+1)
B.20( ﹣1)
﹣1)
C.200
D.300
相关试题

