Question

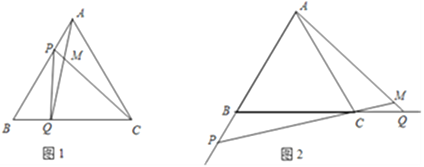
【题目】如图1，点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点，点P从顶点A，点Q从顶点B同时出发，且它们的速度都为1cm／s。

⑴连接AQ、CP交于点M，在点P、Q运动的过程中，∠CMQ的大小变化吗？若变化，则说明理由，若不变，请直接写出它的度数；

⑵点P、Q在运动过程中，设运动时间为t，当t为何值时，△PBQ为直角三角形？

⑶如图2，若点P、Q在运动到终点后继续在射线AB、BC上运动，直线AQ、CP交点为M，则∠CMQ的大小变化吗？则说明理由；若不变，请求出它的度数。

Answer 1

【答案】见解析

【解析】试题分析：（1）因为点P从顶点A，点Q从顶点B同时出发，且它们的速度都为1cm/s，所以AP=BQ．AB=AC，∠B=∠CAP=60°，因而运用边角边定理可知△ABQ≌△CAP．再用全等三角形的性质定理及三角形的角间关系、三角形的外角定理，可求得CQM的度数；

（2）设时间为t，则AP=BQ=t，PB=4-t．分别就①当∠PQB=90°时；②当∠BPQ=90°时利用直角三角形的性质定理求得t的值；

（3）首先利用边角边定理证得△PBC≌△QCA，再利用全等三角形的性质定理得到∠BPC=∠MQC．再运用三角形角间的关系求得∠CMQ的度数．

试题解析：（1）∠CMQ不变．

AC="BA," ∠A=∠B, AP="BQ,"

∴△ACP≌△BAQ, ∴∠ACP=∠BAQ,

∴∠CMQ=∠ACP+∠MAC=∠BAQ+∠MAC=∠BAC=60°．

∴∠CMQ恒等于60°，不发生变化．

（2）设运动了t秒

当△PBQ为Rt三角形时 ∠B="60°"

①当∠BPQ=30°时 ∴PB="AB-BP=4-t=2BQ=2t" 解得t=

②当∠PQB=30°时 则BQ=t=2PB=2（AB-AP）=2（4-t） 解得t=

（3）∠CMQ不变．

∵AC=CB,∠ACQ=120°=∠CBP, CQ="BP,"

∴△ACQ≌△CBP, ∴∠CAQ=∠BCP,

∴∠CMQ=∠CAQ+∠ACM=∠BCP+∠ACM=∠MCQ+∠ACM=∠ACQ=120°．

∴∠CMQ恒等于120°，不会发生变化．