搜索
【题目】在平面直角坐标系中，将抛物线y=x2+2x+3绕着原点旋转180°，所得抛物线的解析式是_____．
参考答案：
【答案】y=﹣(x﹣1)2﹣2
【解析】
先求出抛物线的顶点坐标，再求出该点关于原点的对称点，即可求出旋转后的抛物线解析式．
解：y=x2+2x+3=(x+1)2+2，抛物线y=x2+2x+3的顶点坐标为(﹣1，2)，点(﹣1，2)关于原点的对称点为(1，﹣2)，
所以抛物线y=x2+2x+3绕着原点旋转180°，所得抛物线的解析式是y=﹣(x﹣1)2﹣2．
故答案是：y=﹣(x﹣1)2﹣2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校园商店经销甲、乙两种文具． 现有如下信息:
请根据以上信息，解答下列问题：
（1）甲、乙两种文具的零售单价分别为 元和 元．（直接写出答案）
（2）该校园商店平均每天卖出甲文具50件和乙文具120件．经调查发现，甲种文具零售单价每降0.1元，甲种文具每天可多销售10件．为了降价促销，使学生得到实惠，商店决定把甲种文具的零售单价下降m（m＞0）元．在不考虑其他因素的条件下，当m定为多少时，可以使商店每天销售甲、乙两种文具获取的利润保持不变？
-
科目： 来源： 题型：
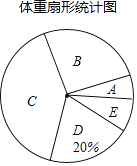
查看答案和解析>>【题目】某校为了解九年级学生的体重情况，随机抽取了九年级部分学生进行调查，将抽取学生的体重情况绘制如下不完整的统计图表，如图表所示，请根据图表信息回答下列问题：
体重频数分布表
组边
体重（千克）
人数
A
45≤x＜50
12
B
50≤x＜55
m
C
55≤x＜60
80
D
60≤x＜65
40
E
65≤x＜70
16
（1）填空：①m=__（直接写出结果）；
②在扇形统计图中，C组所在扇形的圆心角的度数等于__度；
（2）如果该校九年级有1000名学生，请估算九年级体重低于60千克的学生大约有多少人？
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．
（1）当直线MN绕点C旋转到图1的位置时，求证：①△ADC≌△CEB；②DE=AD+BE；
（2）当直线MN绕点C旋转到图2的位置时，求证：DE=AD﹣BE；
（3）当直线MN绕点C旋转到图3的位置时，试问DE、AD、BE具有怎样的等量关系？请写出这个等量关系，并加以证明．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了了解同学们每月零花钱的数额，校园小记者随机调查了本校部分同学，根据调查结果，绘制出了如下两个尚不完整的统计图表．
调查结果统计表
组别
分组（单位：元）
人数
A
0≤x＜30
4
B
30≤x＜60
16
C
60≤x＜90
a
D
90≤x＜120
b
E
x≥120
2
请根据以上图表，解答下列问题：
（1）填空：这次被调查的同学共有__人，a+b=__，m=___；
（2）求扇形统计图中扇形C的圆心角度数；
（3）该校共有学生1000人，请估计每月零花钱的数额x在60≤x＜120范围的人数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况，随机选取该校部分学生进行调查，要求每名学生从中只选一类最喜爱的电视节目.以下是根据调查结果绘制的统计图表的一部分.
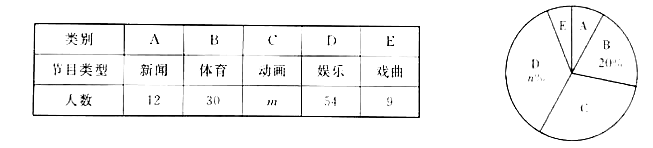
根据以上信息，解答下列问题：
（1）被调查的学生中，最喜爱体育节目的有 人，这些学生数占被调查总人数的百分比为 %；
（2）被调查学生的总数为 人，统计表中
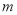的值为 ，统计图中
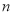的值为 ；（3）在统计图中，
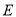类所对应扇形圆心角的度数为 ；（4）该校共有2000名学生，根据调查结果，估计该校最喜爱欣慰节目的学生数.
-
科目： 来源： 题型：
查看答案和解析>>【题目】将方程x2﹣6x＋2=0配方后，原方程变形为（ ）
A. (x+3)2=﹣2B. (x﹣3)2=﹣2C. (x﹣3)2=7D. (x＋3)2=7
相关试题
