【题目】如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以lcm/s的速度运动,同时点F从点B出发沿线射BC以2cm/s的速度运动,设运动时间为t(s). 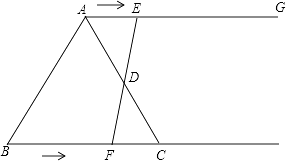
(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;
(2)当t为多少时,四边形ACFE是菱形.
参考答案:
【答案】
(1)证明:∵AG∥BC,
∴∠EAD=∠DCF,∠AED=∠DFC,
∵D为AC的中点,
∴AD=CD,
在△ADE和△CDF中,
 ,
,
∴△ADE≌△CDF(AAS)
(2)解:①若四边形ACFE是菱形,则有CF=AC=AE=6,
则此时的时间t=6÷1=6(s).
故答案为:6s.
【解析】(1)由题意得到AD=CD,再由AG与BC平行,利用两直线平行内错角相等得到两对角相等,利用AAS即可得证;(2)若四边形ACFE是菱形,则有CF=AC=AE=6,由E的速度求出E运动的时间即可.
【考点精析】通过灵活运用等边三角形的性质和菱形的判定方法,掌握等边三角形的三个角都相等并且每个角都是60°;任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.圆中最长的弦是直径B.相等的圆心角所对的弧相等
C.平分弦的直径垂直于弦D.过三个点一定能作一个圆
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简:(x+1)(x﹣1)+1= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】为发展校园足球运动,某城区四校决定联合购买一批足球运动装备.市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.
(1)求每套队服和每个足球的价格是多少元;
(2)若城区四校联合购买100套队服和a(a>10)个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花发费用;
(3)在(2)的条件下,若a=60,假如你是本次购买任务的负责人,你认为到甲、乙哪家商场购买比较合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正比例函数y=kx(k<0)的图象上两点A(x1,y1)、B(x2,y2),且x1<x2,下列说法正确的是( )
A. y1<y2 B. y1>y2 C. y1=y2 D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的两条对角线相交于点O,若AC=8cm,BD=6cm,求菱形的面积和周长各是多少?
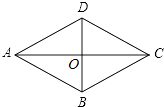
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆锥的底面半径为3,母线长为8,则圆锥的侧面积等于 .
相关试题

