搜索
【题目】观察下列三行数
①﹣3，9，﹣27，81，﹣243，……
②﹣5，7，﹣29，79，﹣245，……
③﹣1，3，﹣9，27，﹣81，……
第①行数排列律是_____；第②行数与第①行数的关系是_____；第③行数与第①行数的关系是_____．
参考答案：
【答案】把一个数乘以﹣3得到它后面的一个数 第②行中的数比第①行中对应位置的数小2 第②行中的数是第①行中对应位置的数乘以
【解析】
仔细观察三行数，寻找其中规律进行解答即可.
（1）﹣3×（﹣3）＝9，9×（﹣3）＝﹣27，﹣27×（﹣3）＝81，81×（﹣3）＝﹣243，因此第①行的排列律是把一个数乘以﹣3得到它后面的一个数；（2）﹣3－2＝﹣5，9－2＝7，﹣27－2＝﹣29，81－2＝79，-243－2＝﹣245，因此第②行数与第①行数的关系是第②行中的数比第①行中对应位置的数小2；（3）-3×＝﹣1,9×＝3，﹣27×＝﹣9，81×＝＝27，-243×＝﹣81，因此第③行数与第①行数的关系是第②行中的数是第①行中对应位置的数乘以.
-
科目： 来源： 题型：
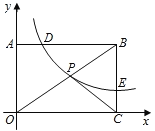
查看答案和解析>>【题目】如图，已知矩形OABC中，OA＝3，AB＝4，双曲线y＝
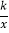（k＞0与矩形两边AB、BC分 别交于点D、E，且BD＝2AD﹒（1）求此双曲线的函数表达式及点E的坐标；
（2）若矩形OABC的对角线OB与双曲线相交于点P，连结PC，求△POC的面积﹒
-
科目： 来源： 题型：
查看答案和解析>>【题目】司机小李某天下午营运全是在东西走向的大道上行驶，如果规定向东行驶为正，向西行驶为负，这天下午行车里程如下：（单位：千米）
，
，
，
，
，
，
，
，
，
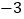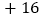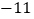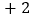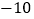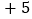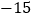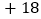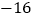
（1）被送到目的地时，小李在出发地的什么位置？
（2若每千米的营运额为8元，则这天下午的营运额为多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC在直角坐标系中，
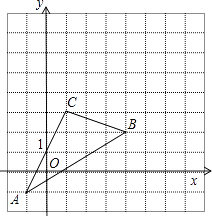
（1）请写出△ABC各点的坐标；
（2）求出S△ABC；
（3）若把△ABC向上平移2个单位，再向右平移2个单位得△A′B′C′，在图中画出△ABC变化位置，并写出A′、B′、C′的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两名队员参加射击训练，成绩分别绘制成下列两个统计图：
根据以上信息，整理分析数据如下：
平均成绩(环)
中位数(环)
众数(环)
方差
甲
a
7
7
1.2
乙
7
b
8
c
（1）写出表格中a，b，c的值；
（2）分别运用表中的四个统计量，简要分析这两名队员的射击成绩，若选派其中一名参赛，你认为应选哪名队员？
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，对于任意一点P（x，y），我们做以下规定：d（P）=|x|+|y|，称d（P）为点P的坐标距离．
（1）已知：点P（3，﹣4），求点P的坐标距离d（P）的值．
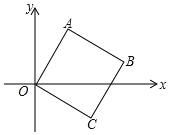
（2）如图，四边形OABC为正方形，且点A、B在第一象限，点C在第四象限．
①求证：d（A）=d（C）．
②若OC=2，且满足d（A）+d（C）=d（B）+2，求点B坐标．
-
科目： 来源： 题型：
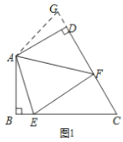
查看答案和解析>>【题目】“半角型”问题探究：如图1，在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°，且∠EAF=60°，探究图中线段BE，EF，FD之间的数量关系.小明同学的方法是将△ABE绕点A逆时针旋转120°到△ADG的位置，然后再证明△AFE≌△AFG，从而得出结论：EF=BE+DF
(1)如图2，在四边形ABCD中，AB=AD，∠B +∠D=180°，E，F分别是边BC，CD上的点，且∠EAF=
∠BAD,上述结论是否仍然成立，并说明理由.(2)实际应用：
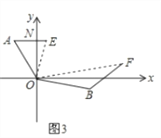
如图3，在某次军事演习中，舰艇甲在指挥中心（O处）北偏西30°的A处，舰艇乙在指挥中心南偏东70°的B处，并且两舰艇到指挥中心的距离相等，接到行动指令后，舰艇甲向正东方向以60海里/小时的速度前进，舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后，指挥中心观测到甲、乙两舰艇分别到达E，F处，且两舰艇之间的夹角为70°，试求此时两舰艇之间的距离？
拓展提高
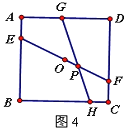
（3）如图4，边长为5的正方形ABCD中，点E、F分别在AB、CD上，AE=CF=1，O为EF的中点，动点G、H分别在边AD、BC上，EF与GH的交点P在O、F之间（与0、F不重合），且∠GPE=45°，设AG=m，求m的取值范围。
相关试题
