【题目】如图,在四边形 ABCD 中,对角线 AC 平分∠DAB,∠ABD=52°,∠ABC=116°,∠ACB=α°,求∠BDC 的度数?

参考答案:
【答案】![]()
【解析】
过C作CE⊥AB于E,CF⊥BD于F,CG⊥AD于G,依据BC平分∠DBE,AC平分∠BAD,即可得到CD平分∠BDG,再根据三角形外角性质,即可得出∠BDC的度数.
解:如图,过C作CE⊥AB于E,CF⊥BD于F,CG⊥AD于G,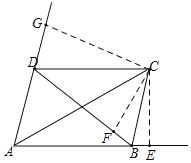
∵∠ABD=52°,∠ABC=116°,
∴∠DBC=∠CBE=64°,
∴BC平分∠DBE,
∴CE=CF,
又∵AC平分∠BAD,
∴CE=CG,
∴CF=CG,
又∵CG⊥AD,CF⊥DB,
∴CD平分∠BDG,
∵∠CBE是△ABC的外角,∠DBE是△ABD的外角,
![]()
∴∠ADB=2∠ACB=2α°,
∴∠BDG=180°-2α°,
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,求∠AEB的度数.
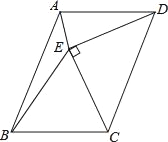
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN周长取最小值时,则∠MPN的度数为_____.
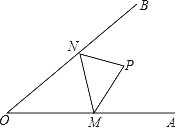
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将长方形纸片ABCD对折后再展开,得到折痕EF,M是BC上一点,沿着AM再次折叠纸片,使得点B恰好落在折痕EF上的点B′处,连接AB′、BB′.

判断△AB′B的形状为 ;
若P为线段EF上一动点,当PB+PM最小时,请描述点P的位置为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级开展征文活动,征文主题只能从“爱国”“敬业”“诚信”“友善”四个主题选择一个,九年级每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行了调查,根据调查结果绘制成如下两幅不完整的统计图.

(1)求共抽取了多少名学生的征文;
(2)将上面的条形统计图补充完整;
(3)在扇形统计图中,选择“爱国”主题所对应的圆心角是多少;
(4)如果该校九年级共有1200名学生,请估计选择以“友善”为主题的九年级学生有多少名.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠ABC=45°,点D是BC边上一动点(与点B,C不重合),点E与点D关于直线AC对称,连结AE,过点B作BF⊥ED的延长线于点F.
(1)依题意补全图形;
(2)当AE=BD时,用等式表示线段DE与BF之间的数量关系,并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正比例函数y=2x与反比例函数y=
 (k>0)的图象交于A、B两点,且点A的横坐标为4,
(k>0)的图象交于A、B两点,且点A的横坐标为4,(1)求k的值;
(2)根据图象直接写出正比例函数值小于反比例函数值时x的取值范围;
(3)过原点O的另一条直线l交双曲线y=
 (k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为224,求点P的坐标.
(k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为224,求点P的坐标.
相关试题

