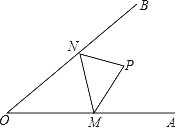
【题目】如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN周长取最小值时,则∠MPN的度数为_____.
参考答案:
【答案】100°
【解析】
分别作点P关于OA、OB的对称点P![]() 、P
、P![]() ,连P
,连P![]() 、P
、P![]() ,交OA于M,交OB于N,△PMN的周长= P
,交OA于M,交OB于N,△PMN的周长= P![]() P
P![]() ,然后得到等腰△OP1P2中,∠O P
,然后得到等腰△OP1P2中,∠O P![]() P
P![]() +∠O P
+∠O P![]() P
P![]() =100°,即可得出∠MPN=∠OPM+∠OPN=∠OP
=100°,即可得出∠MPN=∠OPM+∠OPN=∠OP![]() M+∠OP
M+∠OP![]() N=100°.
N=100°.
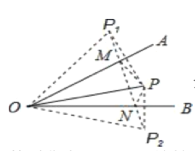
分别作点P关于OA、OB的对称点P![]() 、P
、P![]() ,连接P
,连接P![]() P
P![]() ,交OA于M,交OB于N,则
,交OA于M,交OB于N,则
O P![]() =OP=OP
=OP=OP![]() ,∠OP
,∠OP![]() M=∠MPO,∠NPO=∠NP
M=∠MPO,∠NPO=∠NP![]() O,
O,
根据轴对称的性质,可得MP=P![]() M,PN=P
M,PN=P![]() N,则
N,则
△PMN的周长的最小值=P![]() P
P![]() ,
,
∴∠P![]() OP
OP![]() =2∠AOB=80°,
=2∠AOB=80°,
∴等腰△OP![]() P
P![]() 中,∠OP
中,∠OP![]() P
P![]() +∠OP
+∠OP![]() P
P![]() =100°,
=100°,
∴∠MPN=∠OPM+∠OPN=∠OP![]() M+∠OP
M+∠OP![]() N=100°,
N=100°,
故答案为100°
-
科目: 来源: 题型:
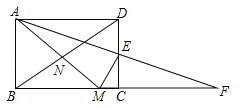
查看答案和解析>>【题目】如图,在矩形ABCD中,AB<BC,E为CD边的中点,将△ADE绕点E顺时针旋转180°,点D的对应点为C,点A的对应点为F,过点E作ME⊥AF交BC于点M,连接AM、BD交于点N,现有下列结论:
①AM=AD+MC;②AM=DE+BM;③DE2=ADCM;④点N为△ABM的外心.其中正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是课本中“作一个角等于已知角”的尺规作图过程.已知:∠AOB. 求作:一个角,使它等于∠AOB.作法:如图
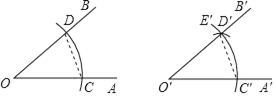
(1)作射线O'A';
(2)以O为圆心,任意长为半径作弧,交OA于C,交OB于D;
(3)以O'为圆心,OC为半径作弧C'E',交O'A'于C';
(4)以C'为圆心,CD为半径作弧,交弧C'E'于D';
(5)过点D'作射线O'B'.
则∠A'O'B'就是所求作的角.
请回答:该作图的依据是( )
A.SSSB.SASC.ASAD.AAS
-
科目: 来源: 题型:
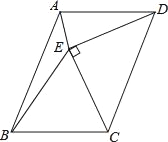
查看答案和解析>>【题目】如图,ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,求∠AEB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将长方形纸片ABCD对折后再展开,得到折痕EF,M是BC上一点,沿着AM再次折叠纸片,使得点B恰好落在折痕EF上的点B′处,连接AB′、BB′.

判断△AB′B的形状为 ;
若P为线段EF上一动点,当PB+PM最小时,请描述点P的位置为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形 ABCD 中,对角线 AC 平分∠DAB,∠ABD=52°,∠ABC=116°,∠ACB=α°,求∠BDC 的度数?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级开展征文活动,征文主题只能从“爱国”“敬业”“诚信”“友善”四个主题选择一个,九年级每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行了调查,根据调查结果绘制成如下两幅不完整的统计图.

(1)求共抽取了多少名学生的征文;
(2)将上面的条形统计图补充完整;
(3)在扇形统计图中,选择“爱国”主题所对应的圆心角是多少;
(4)如果该校九年级共有1200名学生,请估计选择以“友善”为主题的九年级学生有多少名.
相关试题

