【题目】如图,⊙O为△ABC的外接圆,BC为⊙O的直径,BA平分∠CBF,过点A作AD⊥BF,垂足为D.
(1)求证:AD为⊙O的切线;
(2)若BD=1,tan∠BAD= ![]() ,求⊙O的直径.
,求⊙O的直径.
参考答案:
【答案】
(1)证明:连接OA, 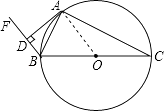
∵BC为⊙O的直径,BA平分∠CBF,AD⊥BF,
∴∠ADB=∠BAC=90°,∠DBA=∠CBA;
∵∠OAC=∠OCA,
∴∠DAO=∠DAB+∠BAO=∠BAO+∠OAC=90°,
∴DA为⊙O的切线
(2)解:∵BD=1,tan∠BAD= ![]() ,
,
∴AD=2,
∴AB= ![]() =
= ![]() ,
,
∴cos∠DBA= ![]() ;
;
∵∠DBA=∠CBA,
∴BC= ![]() =
= ![]() =5.
=5.
∴⊙O的直径为5.
【解析】(1)连接OA,由题意可得∠ADB=∠BAC=90°,再由BA平分∠CBF,可得∠DBA=∠CBA,再由∠OAC=∠OCA,继而可得∠DAO=90°,可证明结论;
(2)由BD=1,tan∠BAD的值可求得AD的值,再由勾股定理可求出AB的值,可求出cos∠DBA的值,在Rt△ABC中由cos∠DBA=![]() 可求出BC的长,可得圆的直径.
可求出BC的长,可得圆的直径.
【考点精析】本题主要考查了圆周角定理和切线的判定定理的相关知识点,需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥CD,过点C作CE∥AD交AB于E,连接AC、DE,AC与DE交于点F.

(1)求证:四边形AECD为平行四边形;
(2)如果EF=2 ,∠FCD=30°,∠FDC=45°,求DC的长.
,∠FCD=30°,∠FDC=45°,求DC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个3×3的方格中填写了9个数字,使得每行、每列、每条对角线上的三个数之和相等,得到的3×3的方格称为一个三阶幻方.
(1)在图1中空格处填上合适的数字,使它构成一个三阶幻方;
(2)如图2的方格中填写了一些数和字母,当x+y的值为多少时,它能构成一个三阶幻方.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y1=x2+2x+m﹣5.
(1)如果该二次函数的图象与x轴有两个交点,求m的取值范围;
(2)如果该二次函数的图象与x轴交于A、B两点,与y轴交于点C,且点B的坐标为(1,0),求它的表达式和点C的坐标;
(3)如果一次函数y2=px+q的图象经过点A、C,请根据图象直接写出y2<y1时,x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线
 经过点A(0,2)和B(1,
经过点A(0,2)和B(1,  ).
).
(1)求该抛物线的表达式;
(2)已知点C与点A关于此抛物线的对称轴对称,点D在抛物线上,且点D的横坐标为4,求点C与点D的坐标;
(3)在(2)的条件下,将抛物线在点A,D之间的部分(含点A,D)记为图象G,如果图象G向下平移t(t>0)个单位后与直线BC只有一个公共点,求t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平整的地面上,10个完全相同的棱长为8cm的小正方体堆成一个几何体.
(1)在下面的网格中画出从左面看和从上面看的形状图.
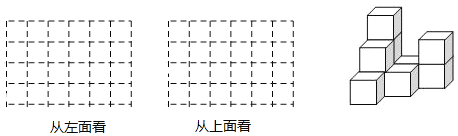
(2)如果在这个几何体的表面(不含底面)喷上黄色的漆,则这个几何体喷漆的面积是多少cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)已知A=3x2+4xy,B=x2+3xy--y2,求:-A+2B.
(2)先化简,再求值:2(5a2-7ab+9b2)-3(14a2-2ab+3b2),其中a=
 ,b=-
,b=- .
.
相关试题

