【题目】已知二次函数y1=x2+2x+m﹣5.
(1)如果该二次函数的图象与x轴有两个交点,求m的取值范围;
(2)如果该二次函数的图象与x轴交于A、B两点,与y轴交于点C,且点B的坐标为(1,0),求它的表达式和点C的坐标;
(3)如果一次函数y2=px+q的图象经过点A、C,请根据图象直接写出y2<y1时,x的取值范围.
参考答案:
【答案】
(1)解:∵二次函数y1=x2+2x+m﹣5的图象与x轴有两个交点,
∴△>0,
∴22﹣4(m﹣5)>0,
解得:m<6
(2)解:∵二次函数y1=x2+2x+m﹣5的图象经过点(1,0),
∴1+2+m﹣5=0,
解得:m=2,
∴它的表达式是y1=x2+2x﹣3,
∵当x=0时,y=﹣3,
∴C(0,﹣3)
(3)解:由图象可知:当y2<y1时,x的取值范围是x<﹣3或x>0.
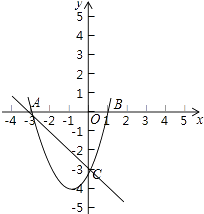
【解析】(1)根据该二次函数的图象与x轴有两个交点可知判别式>0,进而可求出m的范围;
(2)根据该二次函数的图象过点B(1,0),从而求出m的值,可得它的表达式,再由x=0,求得y的值,则可得C的坐标;
(3)根据题意画出图象,再由图象可直接求得.
【考点精析】掌握抛物线与坐标轴的交点是解答本题的根本,需要知道一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现在,苏宁商场进行促销活动,出售一种优惠购物卡(注:此卡只作为购物优惠凭证不能顶替货款),花300元买这种卡后,凭卡可在这家商场按标价的8折购物.
(1)顾客购买多少元金额的商品时,买卡与不买卡花钱相等?在什么情况下购物合算?
(2)小张要买一台标价为3500元的冰箱,如何购买合算?小张能节省多少元钱?
(3)小张按合算的方案,把这台冰箱买下,如果商场还能盈利25%,这台冰箱的进价是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥CD,过点C作CE∥AD交AB于E,连接AC、DE,AC与DE交于点F.

(1)求证:四边形AECD为平行四边形;
(2)如果EF=2 ,∠FCD=30°,∠FDC=45°,求DC的长.
,∠FCD=30°,∠FDC=45°,求DC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个3×3的方格中填写了9个数字,使得每行、每列、每条对角线上的三个数之和相等,得到的3×3的方格称为一个三阶幻方.
(1)在图1中空格处填上合适的数字,使它构成一个三阶幻方;
(2)如图2的方格中填写了一些数和字母,当x+y的值为多少时,它能构成一个三阶幻方.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O为△ABC的外接圆,BC为⊙O的直径,BA平分∠CBF,过点A作AD⊥BF,垂足为D.

(1)求证:AD为⊙O的切线;
(2)若BD=1,tan∠BAD= ,求⊙O的直径.
,求⊙O的直径. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线
 经过点A(0,2)和B(1,
经过点A(0,2)和B(1,  ).
).
(1)求该抛物线的表达式;
(2)已知点C与点A关于此抛物线的对称轴对称,点D在抛物线上,且点D的横坐标为4,求点C与点D的坐标;
(3)在(2)的条件下,将抛物线在点A,D之间的部分(含点A,D)记为图象G,如果图象G向下平移t(t>0)个单位后与直线BC只有一个公共点,求t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平整的地面上,10个完全相同的棱长为8cm的小正方体堆成一个几何体.
(1)在下面的网格中画出从左面看和从上面看的形状图.
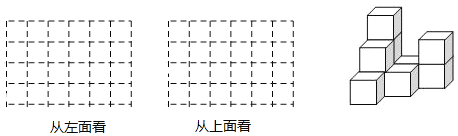
(2)如果在这个几何体的表面(不含底面)喷上黄色的漆,则这个几何体喷漆的面积是多少cm2.
相关试题

