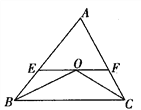
【题目】已知:如图,∠ABC和∠ACB的平分线交于点O,EF经过点O且平行于BC,分别与AB,AC交于点E,F.
(1)若∠ABC=50°,∠ACB=60°,求∠BOC的度数;
(2)若∠ABC=,∠ACB=,用,的代数式表示∠BOC的度数.
(3)在第(2)问的条件下,若∠ABC和∠ACB邻补角的平分线交于点O,其他条件不变,请画出相应图形,并用,的代数式表示∠BOC的度数.
参考答案:
【答案】(1)∠BOC=125°;(2)![]() ;(3)
;(3)![]()
【解析】
试题(1)先根据角平分线的定义求出∠OBC+∠OCB的度数,再根据三角形内角和定理求出∠BOC的度数即可;
(2)先用α、β表示出∠OBC+∠OCB的度数,再根据三角形内角和定理求出∠BOC的度数即可;
(3)根据题意画出图形,再根据三角平分线的定义求出∠CBO+∠ACO的度数,进而可得出结论.
试题解析:(1)∵∠ABC和∠ACB的平分线交于点O,∠ABC=50°,∠ACB=60°,
∴∠OBC+∠OCB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×(50°+60°)=55°,
×(50°+60°)=55°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-55°=125°;
(2)∵∠ABC和∠ACB的平分线交于点O,∠ABC=α,∠ACB=β,
∴∠OBC+∠OCB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() (α+β),
(α+β),
∴∠BOC=180°-(∠OBC+∠OCB)=180°-![]() (α+β);
(α+β);
(3)如图所示:
∵∠ABC和∠ACB邻补角的平分线交于点O,
∴∠CBO+∠BCO= 180°-![]() α+ 180°-
α+ 180°-![]() β=180°-
β=180°- ![]() (α+β),
(α+β),
∴∠BOC=180°-[180°-![]() (α+β)]=
(α+β)]=![]() α+
α+ ![]() β.
β.

-
科目: 来源: 题型:
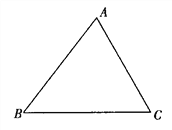
查看答案和解析>>【题目】如图(1)中,△ABC和△ADE都是等腰直角三角形,∠ACB和∠D都是直角,点C在AE上,△ABC绕着A点经过逆时针旋转后能够与△ADE重合,再将图(1)作为“基本图形”绕着A点经过逆时针旋转得到图(2).两次旋转的角度分别为( )

A.45°,90°B.90°,45°C.60°,30°D.30°,60°
-
科目: 来源: 题型:
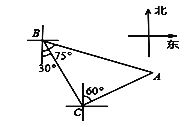
查看答案和解析>>【题目】轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在C处观测灯塔A位于北偏东60°方向上,则C处与灯塔A的距离是( )海里.
A.50B.25C.25
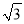 D.25
D.25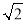
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学学习中,及时对知识进行归纳和整理是改善学习的重要方法.善于学习的小明在学习了一次方程(组).一元一次不等式和一次函数后,对相关知识进行了归纳整理.
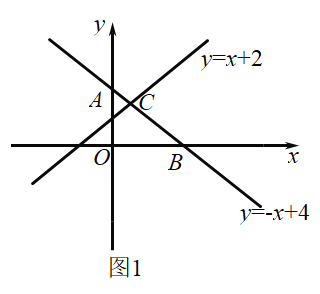
(1)例如,他在同一个直角坐标系中画出了一次函数y=x+2和y=-x+4的图像(如图1),并作了归纳:
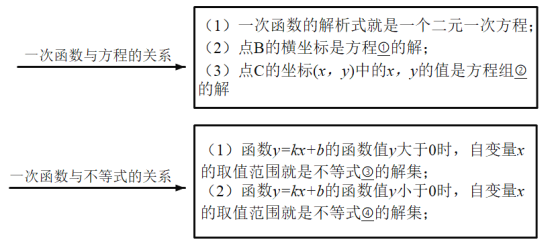
请根据图1和以上方框中的内容,在下面数字序号后写出相应的结论:
① ;② ;
③ ;④ ;
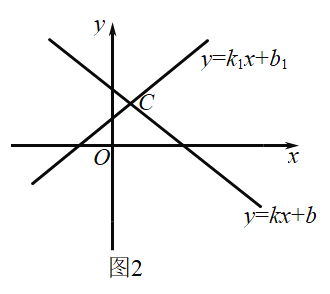
(2)若已知一次函数y=k1x+b1和y=kx+b的图像(如图2),且它们的交点C的坐标为(1,3),那么不等式kx+b≥k1x+b1的解集 .
-
科目: 来源: 题型:
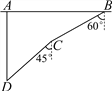
查看答案和解析>>【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AC∥BD,折线AMB夹在两条平行线间.(1)判断∠M,∠A,∠B的关系;(2)请你尝试改变问题中的某些条件,探索相应的结论.建议:①折线中折线段数量增加到n条(n=3,4,…);
②可如图1,图2,或M点在平行线外侧.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
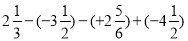 ;
;(2)
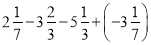 ;
;(3)
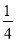 +(-
+(-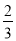 )+
)+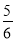 +(-
+(-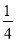 )+ (-
)+ (-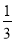 );
);(4)5.6+(-0.9)+4.4+(-8.1)+(-1);
(5)(-3
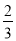 )-(-1
)-(-1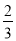 )-(-2
)-(-2 )+(-1.75);
)+(-1.75);(6)-108-(-112)+23+18.
相关试题

