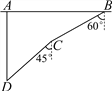
【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).
参考答案:
【答案】拦截点D处到公路的距离是(500+500![]() )米.
)米.
【解析】试题分析:过B作AB的垂线,过C作AB的平行线,两线交于点E;过C作AB的垂线,过D作AB的平行线,两线交于点F,则∠E=∠F=90°,拦截点D处到公路的距离DA=BE+CF.解Rt△BCE,求出BE=![]() BC=
BC=![]() ×1000=500米;解Rt△CDF,求出CF=
×1000=500米;解Rt△CDF,求出CF=![]() CD=500
CD=500![]() 米,则DA=BE+CF=(500+500
米,则DA=BE+CF=(500+500![]() )米.
)米.
试题解析:如图,过B作AB的垂线,过C作AB的平行线,两线交于点E;过C作AB的垂线,过D作AB的平行线,两线交于点F,则∠E=∠F=90°,拦截点D处到公路的距离DA=BE+CF.
在Rt△BCE中,∵∠E=90°,∠CBE=60°,
∴∠BCE=30°,
∴BE=![]() BC=
BC=![]() ×1000=500米;
×1000=500米;
在Rt△CDF中,∵∠F=90°,∠DCF=45°,CD=BC=1000米,
∴CF=![]() CD=500
CD=500![]() 米,
米,
∴DA=BE+CF=(500+500![]() )米,
)米,
故拦截点D处到公路的距离是(500+500![]() )米.
)米.

-
科目: 来源: 题型:
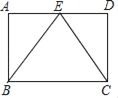
查看答案和解析>>【题目】如图,在矩形ABCD中,点E是边AD的中点,连接BE、CE.
(1)求证:△ABE≌△DCE;
(2)当BC=2AB,求∠BEC的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,点A、B分别在x、y轴上,点B的坐标为(0,1),∠BAO=30°.
(1)求AB的长度;
(2)以AB为一边作等边△ABE,作OA的垂直平分线MN交AB的垂线AD于点D.求证:BD=OE;
(3)在(2)的条件下,连接DE交AB于F.求证:F为DE的中点.



-
科目: 来源: 题型:
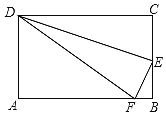
查看答案和解析>>【题目】如图所示,沿DE折叠长方形ABCD的一边,使点C落在AB边上的点F处,若AD=8,且△AFD的面积为60,则△DEC的面积为( )
A.
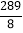
B.
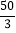
C. 18
D. 20
-
科目: 来源: 题型:
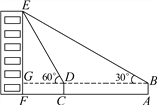
查看答案和解析>>【题目】如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(结果精确到0.1米)
-
科目: 来源: 题型:
查看答案和解析>>【题目】李晖到“宇泉牌”服装专卖店做社会调查.了解到商店为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:
营业员
小俐
小花
月销售件数(件)
200
150
月总收入(元)
1400
1250
假设月销售件数为
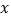 件,月总收入为
件,月总收入为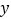 元,销售每件奖励
元,销售每件奖励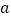 元,营业员月基本工资为
元,营业员月基本工资为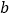 元.
元.(1)求
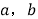 的值;
的值;(2)若营业员小俐某月总收入不低于
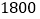 元,那么小俐当月至少要卖服装多少件?
元,那么小俐当月至少要卖服装多少件? -
科目: 来源: 题型:
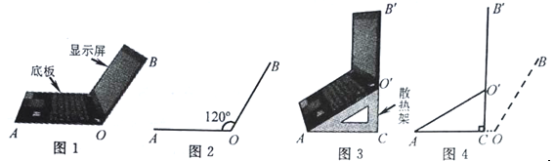
查看答案和解析>>【题目】小红将笔记本电脑水平放置在桌子上,显示屏OB与底板OA所在水平线的夹角为120°时,感觉最舒适(如图1),侧面示意图为图2;使用时为了散热,她在底板下面垫入散热架ACO'后,电脑转到AO'B'位置(如图3),侧面示意图为图4.已知OA=OB=24cm,O'C⊥OA于点C,O'C=12cm.
(1)求∠CAO'的度数.
(2)显示屏的顶部B'比原来升高了多少?
(3)如图4,垫入散热架后,要使显示屏O'B'与水平线的夹角仍保持120°,则显示屏O'B'应绕点O'按顺时针方向旋转多少度?
相关试题

