【题目】如图,梯形OABC中,BC∥AO,O(0,0),A(10,0),B(10,4),BC=2,G(t,0)是底边OA上的动点. 
(1)tan∠OAC= .
(2)边AB关于直线CG的对称线段为MN,若MN与△OAC的其中一边平行时,则t=
参考答案:
【答案】
(1)2
(2)4或4 ![]() 或10﹣2
或10﹣2 ![]()
【解析】解:(1)∵BC∥AO,
∴∠OAC=∠ACB,
∵AB=4,BC=2,
∴tan∠OAC=tan∠ACB= ![]() =
= ![]() =2.
=2.
所以答案是2.
2)情形①图1中,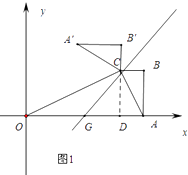
当A′B′∥OA时,作CD⊥OA垂足为D,
∵∠BCB′=90°,CG平分∠BCB′,
∴∠GCD=∠NCB′=45°
∴△CGD是等腰直角三角形,
∴DG=CD=4,t=OG=OD﹣GD=8﹣4=4.
情形②图2中,A′B′∥AC,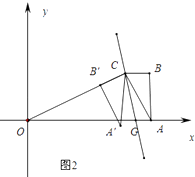
∵OC=4 ![]() ,AC=2
,AC=2 ![]() ,AO=10,
,AO=10,
∴AO2=OC2+AC2 ,
∴∠OCA=90°,
∵A′B′∥AC,∠A′B′C=90°,
∴点B′在线段OC上,
∵CG平分∠BCB′,BC∥OA,
∴∠BCG=∠OGC=∠OCG,
∴OG=OC= ![]() =4
=4 ![]() ,
,
∴t=4 ![]() .
.
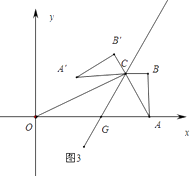
情形③图3中,A′B′∥OC时,
∵CG平分∠BCB′,BC∥OA,
∴∠ACG=∠B′CE=′BCE=′AGC,
∴AG=AC= ![]() =2
=2 ![]() ,
,
∴t=CG=AO﹣AG=10﹣2 ![]() .
.
所以答案是4或4 ![]() 或10﹣2
或10﹣2 ![]() .
.
【考点精析】利用梯形的定义和轴对称的性质对题目进行判断即可得到答案,需要熟知一组对边平行,另一组对边不平行的四边形是梯形.两腰相等的梯形是等腰梯形;关于某条直线对称的两个图形是全等形;如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线;两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用大小相同的小三角形摆成如图所示的图案,按照这样的规律摆放,则第n个图案中共有小三角形的个数是 .
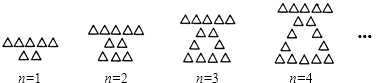
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,直线y=2x+m与y轴交于点A,与直线y=-x+5交于点B(4,n),P为直线y=-x+5上一点.
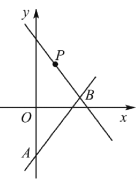
(1)求m,n的值;
(2)求线段AP的最小值,并求此时点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义一种新运算“⊕”:a⊕b=2a﹣ab,比如1⊕(﹣3)=2×1﹣1×(﹣3)=5
(1)求(﹣2)⊕3的值;
(2)若(﹣3)⊕x=(x+1)⊕5,求x的值;
(3)若x⊕1=2(1⊕y),求代数式
 x+y+1的值.
x+y+1的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
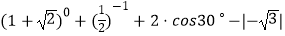 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列变形中:
①由方程
 =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;②由方程
 x=
x= 两边同除以
两边同除以 ,得x=1;
,得x=1;③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣
 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】同学们,足球是世界上第一大运动,你热爱足球运动吗?已知在足球比赛中,胜一场得3分,平一场得1分,负一场得0分,一队共踢了30场比赛,负了9场,共得47分,那么这个队胜了( )
A. 10场 B. 11场 C. 12场 D. 13场
相关试题

