【题目】如图,矩形纸片ABCD中,AB=3cm,现将纸片折叠压平,使点A与点C重合,折痕为EF,如果sin∠BAE= ![]() ,那么重叠部分△AEF的面积为( )
,那么重叠部分△AEF的面积为( ) 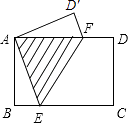
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】B
【解析】解:设AE=13x,则BE=5x,由折叠可知,EC=13x, 在Rt△ABE中,AB2+BE2=AE2 ,
即32+(5x)2=(13x)2 ,
解得:x= ![]() ,
,
由折叠可知∠AEF=∠CEF,
∵AD∥BC,
∴∠CEF=∠AFE,
∴∠AEF=∠AFE,即AE=AF= ![]() ,
,
∴S△AEF= ![]() ×AF×AB=
×AF×AB= ![]() ×
× ![]() ×3=
×3= ![]() ;
;
故选:B.
【考点精析】通过灵活运用翻折变换(折叠问题)和解直角三角形,掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班计划购买篮球和排球若干个,买4个篮球和3个排球需要410元;买2个篮球和5个排球需要310元.
(1)篮球和排球单价各是多少元?
(2)若两种球共买30个,费用不超过1700元,篮球最多可以买多少个?
(3)如果购买这两种球刚好用去520元,问有哪几种购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,线段AB⊥BC于点B,CD⊥BC于点C,点E在线段BC上,且AE⊥DE.
(1)求证:∠EAB=∠CED;
(2)如图2,AF、DF分别平分∠BAE和∠CDE,EH平分∠DEC交CD于点H,EH的反向延长线交AF于点G.
①求证EG⊥AF;
②求∠F的度数.(提示:三角形内角和等于180度)
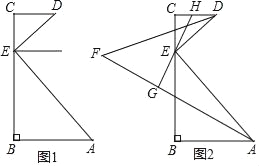
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分9分)小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发
的同时,他的爸爸以96m/min速度从邮局同一条道路步行回家,小明在邮局停留2min后沿原路
以原速返回,设他们出发后经过t min时,小明与家之间的距离为s1 m,小明爸爸与家之间的距
离为s2 m,图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象.
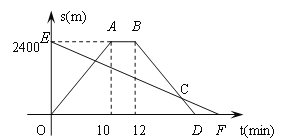
(1)求s2与t之间的函数关系式;
(2)小明从家出发,经过多长时间在返回途中追上爸爸?这时他们距离家还有多远?
-
科目: 来源: 题型:
查看答案和解析>>【题目】骰子是一种特别的数字立方体(如图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是( ).

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAC=90°,AD⊥BC,垂足为D,则下面的结论中正确的个数为( )
①AB与AC互相垂直;
②AD与AC互相垂直;
③点C到AB的垂线段是线段AB;
④线段AB的长度是点B到AC的距离;
⑤线段AB是B点到AC的距离.

A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,DB=DC,∠C的度数比∠ABD的度数大54°,AE⊥BD于点E,则∠DAE的度数等于 .
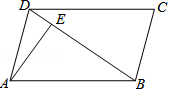
相关试题

