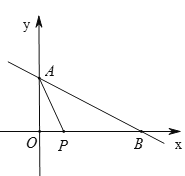
【题目】如图,已知一次函数![]() 与两坐标分别交于
与两坐标分别交于![]() 两点,动点
两点,动点![]() 从原点
从原点![]() 出发,以每秒2个单位长度的速度沿
出发,以每秒2个单位长度的速度沿![]() 轴正方向运动,连接
轴正方向运动,连接![]() .设运动时间为
.设运动时间为![]() s.
s.
(1)当![]() 为何值时,
为何值时,![]() 的面积为6?
的面积为6?
(2)若![]() ,作
,作![]() 中边
中边![]() 上的高
上的高![]() ,当
,当![]() 为何值时,
为何值时,![]() 长为4?并直接写出此时点
长为4?并直接写出此时点![]() 的坐标.
的坐标.
参考答案:
【答案】(1) ![]() 或
或![]() ;(2)
;(2) ![]()
![]() .
.
【解析】
(1)先求出A、B两点的坐标,再分点P在B点左侧与右侧两种情况进行讨论即可;
(2)作△PAB中AP边上的高BQ,先根据AAS得出△AOP≌△BQP,再由勾股定理得出t的值,继而得出结论即可.
(1)当x=0时,![]() =4,
=4,
当y=0时,0=![]() ,解得:x=8,
,解得:x=8,
∴A(0,4),B(8,0),
即AO=4,OB=8,
∵△PAB的面积为6,
∴![]() PBAO=6,
PBAO=6,
∴PB=3,
∵OP=2t,
∴当点P在点B的左侧时,PB=8-2t;当点P在点B的右侧时,PB=2t-8;
即8-2t=3或2t-8=3,
∴![]() 或
或![]() ;
;
(2) 作△PAB中AP边上的高BQ,
在△AOP和△BQP中
 ,
,
∴△AOP≌△BQP,
∴AP=BP,
在Rt△AOP中,OP2+OA2=AP2,
即42+(2t)2=(8-2t)2,
解得t=![]() ,
,
∴当t=![]() 时,BQ的长为4,
时,BQ的长为4,
作QH⊥OB于H,则有HQ//OA,
∴△PHQ∽△POA,
∴![]() ,
,
∴![]() ,
,
∴HQ=![]() ,PH=
,PH=![]() ,
,
∴OH=OP+PH=![]() ,
,
∴Q![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,长方形
 的顶点
的顶点 在坐标原点,顶点
在坐标原点,顶点 分别在
分别在 轴,
轴, 轴的正半轴上,
轴的正半轴上, ,
, 为边
为边 的中点,
的中点, 是边
是边 上的一个动点,当
上的一个动点,当 的周长最小时,点
的周长最小时,点 的坐标为_________.
的坐标为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的网格中建立平面直角坐标系后,
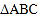 三个顶点的坐标分别为
三个顶点的坐标分别为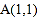 ,
,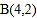 ,
,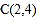 .
.(1)画出
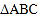 关于
关于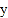 轴的对称图形
轴的对称图形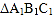 ;
;(2)借助图中的网格,请只用直尺(不含刻度)完成以下要求:(友情提醒:请别忘了标注字母)
①在图中找一点
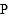 ,使得
,使得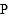 到边
到边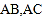 的距离相等,且
的距离相等,且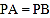 ;
;②在
 轴上找一点
轴上找一点 ,使得
,使得 的周长最小,并求出此时点
的周长最小,并求出此时点 的坐标.
的坐标.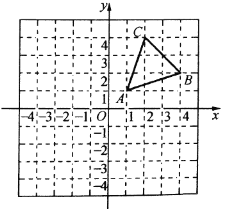
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,元旦期间,小明乘汽车从
 地出发,经过
地出发,经过 地到目的地
地到目的地 地(三地在同一条直线上),假设汽车从
地(三地在同一条直线上),假设汽车从 到
到 的过程都是匀速直线行驶.图②表示小明离
的过程都是匀速直线行驶.图②表示小明离 地的路程
地的路程 (km)与汽车从
(km)与汽车从 出发后行驶时间
出发后行驶时间 (h)之何的函数关系图像.
(h)之何的函数关系图像.(1)
 两地间的路程为 km;
两地间的路程为 km;(2)求小明离
 地的路程
地的路程 与行驶时间
与行驶时间 之间的函数表达式;
之间的函数表达式;(3)当行驶时间
 在什么范围时,汽车离
在什么范围时,汽车离 地的路程不超过40 km?
地的路程不超过40 km?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两地之间有一条笔直的公路
 ,小明从甲地出发沿公路
,小明从甲地出发沿公路 步行前往乙地,同时小亮从乙地出发沿公路
步行前往乙地,同时小亮从乙地出发沿公路 骑车前往甲地,小亮到达甲地停留一段时间,原路原速返回,追上小明后两人一起步行到乙地.设小明与甲地的距离为
骑车前往甲地,小亮到达甲地停留一段时间,原路原速返回,追上小明后两人一起步行到乙地.设小明与甲地的距离为 (m),小亮与甲地的距离为
(m),小亮与甲地的距离为 (m),小明与小亮之间的距离为
(m),小明与小亮之间的距离为 (m),小明行走的时间为
(m),小明行走的时间为 (min).
(min). ,
, 与
与 之间的函数图象如图①,
之间的函数图象如图①, 与
与 之间的函数图象(部分)如图②.
之间的函数图象(部分)如图②.(1)求小亮从乙地到甲地过程中
 (m)与
(m)与 (min)之间的函数表达式;
(min)之间的函数表达式;(2)求小亮从甲地返回到与小明相遇的过程中
 (m)与
(m)与 ( min)之间的函数表达式;
( min)之间的函数表达式;(3)在图②中,补全整个过程中
 (m)与
(m)与 (min)之间的函数图象,并确定
(min)之间的函数图象,并确定 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小龙在学校组织的社会调查活动中负责了解他所居住的小区450户居民的家庭收入情况. 他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.
分组
频数
百分比
600≤
 <800
<8002
5%
800≤
 <1000
<10006
15%
1000≤
 <1200
<120045%
9
22.5%
1600≤
 <1800
<18002
合计
40
100%

根据以上提供的信息,解答下列问题:
(1)补全频数分布表.
(2)补全频数分布直方图.
(3)绘制相应的频数分布折线图.
(4)请你估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明为了了解气温对用电量的影响,对去年自己家的每月用电量和当地气温进行了统计.当地去年每月的平均气温如图1,小明家去年月用电量如图2.
根据统计表,回答问题:
(1)当地去年月平均气温的最高值、最低值各为多少?相应月份的用电量各是多少?
(2)请简单描述月用电量与气温之间的关系;
(3)假设去年小明家用电量是所在社区家庭年用电量的中位数,据此他能否预测今年该社区的年用电量?请简要说明理由.
相关试题

