【题目】如图①,元旦期间,小明乘汽车从![]() 地出发,经过
地出发,经过![]() 地到目的地
地到目的地![]() 地(三地在同一条直线上),假设汽车从
地(三地在同一条直线上),假设汽车从![]() 到
到![]() 的过程都是匀速直线行驶.图②表示小明离
的过程都是匀速直线行驶.图②表示小明离![]() 地的路程
地的路程![]() (km)与汽车从
(km)与汽车从![]() 出发后行驶时间
出发后行驶时间![]() (h)之何的函数关系图像.
(h)之何的函数关系图像.
(1)![]() 两地间的路程为 km;
两地间的路程为 km;
(2)求小明离![]() 地的路程
地的路程![]() 与行驶时间
与行驶时间![]() 之间的函数表达式;
之间的函数表达式;
(3)当行驶时间![]() 在什么范围时,汽车离
在什么范围时,汽车离![]() 地的路程不超过40 km?
地的路程不超过40 km?

参考答案:
【答案】(1)160;(2)当![]() 时,表达式为:
时,表达式为:![]() ,当
,当![]() 时,表达式为:
时,表达式为:![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据图象中的数据即可得到A,C两地的距离;
(2)根据函数图象中的数据即可得到小明离![]() 地的路程
地的路程![]() 与行驶时间
与行驶时间![]() 之间的函数表达式;
之间的函数表达式;
(3)根据题意可以分到B地前和到B地前后两种情况进行解答.
(1)由题意和图象可得,
A,C两地相距:120+40=160千米,
故答案为:160;
(2) 当![]() 时,设路程
时,设路程![]() 与行驶时间
与行驶时间![]() 之间的函数表达式:y=kx+b,
之间的函数表达式:y=kx+b,
由图象过点![]() 可得:
可得:
![]() 得
得![]()
当![]() 时,路程
时,路程![]() 与行驶时间
与行驶时间![]() 之间的函数表达式为:
之间的函数表达式为:![]() ,
,
由于速度不变,经过B地到大C地的时间为:![]()
当![]() 时,路程
时,路程![]() 与行驶时间
与行驶时间![]() 之间的函数表达式为:
之间的函数表达式为:![]() ;
;
(3)由题意可得,![]()
当行驶时间![]() 时,汽车离
时,汽车离![]() 地的路程不超过40 km.
地的路程不超过40 km.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级(1)班为了了解同学们一天零花钱的消费情况,对本班同学开展了调查,将同学一周的零花钱以2元为组距,绘制如图的频率分布直方图,已知从左到右各组的频数之比为2∶3∶4∶2∶1.

(1)若该班有48人,则零花钱用最多的是第_____组,有_______人;
(2)零花钱在8元以上的共有_____人;
(3)若每组的平均消费按最大值计算,则该班同学的日平均消费额是_______元(精确到0.1元)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,长方形
 的顶点
的顶点 在坐标原点,顶点
在坐标原点,顶点 分别在
分别在 轴,
轴, 轴的正半轴上,
轴的正半轴上, ,
, 为边
为边 的中点,
的中点, 是边
是边 上的一个动点,当
上的一个动点,当 的周长最小时,点
的周长最小时,点 的坐标为_________.
的坐标为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的网格中建立平面直角坐标系后,
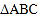 三个顶点的坐标分别为
三个顶点的坐标分别为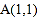 ,
,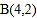 ,
,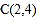 .
.(1)画出
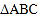 关于
关于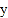 轴的对称图形
轴的对称图形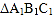 ;
;(2)借助图中的网格,请只用直尺(不含刻度)完成以下要求:(友情提醒:请别忘了标注字母)
①在图中找一点
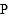 ,使得
,使得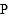 到边
到边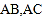 的距离相等,且
的距离相等,且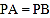 ;
;②在
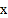 轴上找一点
轴上找一点 ,使得
,使得 的周长最小,并求出此时点
的周长最小,并求出此时点 的坐标.
的坐标.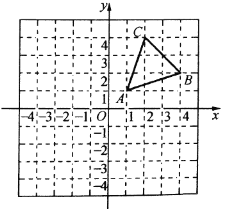
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数
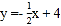 与两坐标分别交于
与两坐标分别交于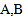 两点,动点
两点,动点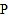 从原点
从原点 出发,以每秒2个单位长度的速度沿
出发,以每秒2个单位长度的速度沿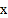 轴正方向运动,连接
轴正方向运动,连接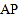 .设运动时间为
.设运动时间为 s.
s.(1)当
 为何值时,
为何值时,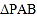 的面积为6?
的面积为6?(2)若
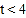 ,作
,作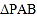 中边
中边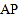 上的高
上的高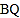 ,当
,当 为何值时,
为何值时,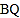 长为4?并直接写出此时点
长为4?并直接写出此时点 的坐标.
的坐标.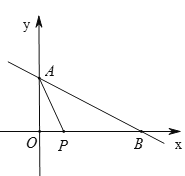
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两地之间有一条笔直的公路
 ,小明从甲地出发沿公路
,小明从甲地出发沿公路 步行前往乙地,同时小亮从乙地出发沿公路
步行前往乙地,同时小亮从乙地出发沿公路 骑车前往甲地,小亮到达甲地停留一段时间,原路原速返回,追上小明后两人一起步行到乙地.设小明与甲地的距离为
骑车前往甲地,小亮到达甲地停留一段时间,原路原速返回,追上小明后两人一起步行到乙地.设小明与甲地的距离为 (m),小亮与甲地的距离为
(m),小亮与甲地的距离为 (m),小明与小亮之间的距离为
(m),小明与小亮之间的距离为 (m),小明行走的时间为
(m),小明行走的时间为 (min).
(min). ,
, 与
与 之间的函数图象如图①,
之间的函数图象如图①, 与
与 之间的函数图象(部分)如图②.
之间的函数图象(部分)如图②.(1)求小亮从乙地到甲地过程中
 (m)与
(m)与 (min)之间的函数表达式;
(min)之间的函数表达式;(2)求小亮从甲地返回到与小明相遇的过程中
 (m)与
(m)与 ( min)之间的函数表达式;
( min)之间的函数表达式;(3)在图②中,补全整个过程中
 (m)与
(m)与 (min)之间的函数图象,并确定
(min)之间的函数图象,并确定 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小龙在学校组织的社会调查活动中负责了解他所居住的小区450户居民的家庭收入情况. 他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.
分组
频数
百分比
600≤
 <800
<8002
5%
800≤
 <1000
<10006
15%
1000≤
 <1200
<120045%
9
22.5%
1600≤
 <1800
<18002
合计
40
100%

根据以上提供的信息,解答下列问题:
(1)补全频数分布表.
(2)补全频数分布直方图.
(3)绘制相应的频数分布折线图.
(4)请你估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户?
相关试题

