【题目】如图,点E在以AB为直径的⊙O上,点C是 ![]() 的中点,过点C作CD垂直于AE,交AE的延长线于点D,连接BE交AC于点F.
的中点,过点C作CD垂直于AE,交AE的延长线于点D,连接BE交AC于点F. 
(1)求证:CD是⊙O的切线;
(2)若cos∠CAD= ![]() ,BF=15,求AC的长.
,BF=15,求AC的长.
参考答案:
【答案】
(1)证明:连接OC,如图1所示.
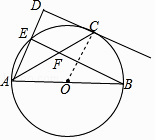
∵点C是 ![]() 的中点,
的中点,
∴ ![]() =
= ![]() ,
,
∴OC⊥BE.
∵AB是⊙O的直径,
∴AD⊥BE,
∴AD∥OC.
∵AD⊥CD,
∴OC⊥CD,
∴CD是⊙O的切线.
(2)解:过点O作OM⊥AC于点M,如图2所示.

∵点C是 ![]() 的中点,
的中点,
∴ ![]() =
= ![]() ,∠BAC=∠CAE,
,∠BAC=∠CAE,
∴ ![]() =
= ![]() .
.
∵cos∠CAD= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴AB= ![]() BF=20.
BF=20.
在Rt△AOM中,∠AMO=90°,AO= ![]() AB=10,cos∠OAM=cos∠CAD=
AB=10,cos∠OAM=cos∠CAD= ![]() ,
,
∴AM=AOcos∠OAM=8,
∴AC=2AM=16.
【解析】(1)连接OC,由点C是 ![]() 的中点利用垂径定理可得出OC⊥BE,由AB是⊙O的直径可得出AD⊥BE,进而可得出AD∥OC,再根据AD⊥CD可得出OC⊥CD,由此即可证出CD是⊙O的切线.(2)过点O作OM⊥AC于点M,由点C是
的中点利用垂径定理可得出OC⊥BE,由AB是⊙O的直径可得出AD⊥BE,进而可得出AD∥OC,再根据AD⊥CD可得出OC⊥CD,由此即可证出CD是⊙O的切线.(2)过点O作OM⊥AC于点M,由点C是 ![]() 的中点利用圆周角定理可得出∠BAC=∠CAE,根据角平分线的定理结合cos∠CAD=
的中点利用圆周角定理可得出∠BAC=∠CAE,根据角平分线的定理结合cos∠CAD= ![]() 可求出AB的长度,在Rt△AOM中,通过解直角三角形可求出AM的长度,再根据垂径定理即可得出AC的长度.
可求出AB的长度,在Rt△AOM中,通过解直角三角形可求出AM的长度,再根据垂径定理即可得出AC的长度.
【考点精析】本题主要考查了解直角三角形的相关知识点,需要掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学九(2)班同学为了了解2019年某小区家庭月均用水情况,随机调查了该小区的部分家庭,并将调查数据进行如下整理:
月均用水量
 (吨)
(吨)频数
频率

6
0.12

________
0.24

16
0.32

10
0.20
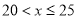
4
________

2
0.04

请解答以下问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)月均用水量的中位数落在第________小组;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20吨的家庭大约有多少户?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E,

(1)求证:DE=DB;
(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】你能求(x﹣1)(x99+x98+x97+…+x+1)的值吗?
遇到这样的问题,我们可以先思考一下,从简单的情形入手.先计算下列各式的值:
(1)(x﹣1)(x+1)= ;
(2)(x﹣1)(x2+x+1)= ;
(3)(x﹣1)(x3+x2+x+1)= ;
由此我们可以得到(x﹣1)(x99+x98+…+x+1)= ;
请你利用上面的结论,完成下面两题的计算:
(1)299+298+…+2+1;
(2)(﹣3)50+(﹣3)49+…+(﹣3)+1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC.
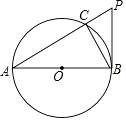
(1)求证:∠BAC=∠CBP;
(2)求证:PB2=PCPA;
(3)当AC=6,CP=3时,求sin∠PAB的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F.

(1)求证:DE是⊙O的切线;
(2)若CF=2,DF=4,求⊙O直径的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市是蜜桔之乡,今年桔子大丰收,某合作社要把240吨桔子运往某市的A、B两地,用大、小两种货车共20辆,恰好能一次性运完这批桔子,已知这两种货车的载重量分别为15吨/辆和10吨/辆.
(1)这两种货车各有多少辆?
(2)运往A地的运费为:大车630元/辆,小车420元/辆;运往B地的运费为:大车750元/辆,小车550元/辆.若把20辆货车中的10辆安排前往A地,其余货车前往B地,其中调往A地的大车有a辆,求总运费.(用含a的式子表示)
相关试题

