【题目】在△ABC中,M是AC边上的一点,连接BM.将△ABC沿AC翻折,使点B落在点D处,当DM∥AB时,求证:四边形ABMD是菱形. 
参考答案:
【答案】证明:∵AB∥DM, ∴∠BAM=∠AMD,
∵△ADC是由△ABC翻折得到,
∴∠CAB=∠CAD,AB=AD,BM=DM,
∴∠DAM=∠AMD,
∴DA=DM=AB=BM,
∴四边形ABMD是菱形.
【解析】只要证明AB=BM=MD=DA,即可解决问题.
【考点精析】本题主要考查了菱形的判定方法和翻折变换(折叠问题)的相关知识点,需要掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)计算:6cos45°+( )﹣1+(
)﹣1+(  ﹣1.73)0+|5﹣3
﹣1.73)0+|5﹣3  |+42017×(﹣0.25)2017
|+42017×(﹣0.25)2017
(2)先化简,再求值:( ﹣a+1)÷
﹣a+1)÷  +
+  ﹣a,并从﹣1,0,2中选一个合适的数作为a的值代入求值.
﹣a,并从﹣1,0,2中选一个合适的数作为a的值代入求值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将平行四边形ABCD沿对角线BD折叠,使点A落在点A'处.若∠1=∠2=50°,则∠A'为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】校园广播主持人培训班开展比赛活动,分为 A、B、C、D四个等级,对应的成绩分别是9分、8分、7分、6分,根据如图不完整的统计图解答下列问题:

(1)补全下面两个统计图(不写过程);
(2)求该班学生比赛的平均成绩;
(3)现准备从等级A的4人(两男两女)中随机抽取两名主持人,请利用列表或画树状图的方法,求恰好抽到一男一女学生的概率? -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店分两次购进 A、B两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
购进数量(件)
购进所需费用(元)
A
B
第一次
30
40
3800
第二次
40
30
3200
(1)求A、B两种商品每件的进价分别是多少元?
(2)商场决定A种商品以每件30元出售,B种商品以每件100元出售.为满足市场需求,需购进A、B两种商品共1000件,且A种商品的数量不少于B种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板Rt△ABD与Rt△ACB(其中∠ABD=90°,∠D=60°,∠ACB=90°,∠ABC=45°)如图摆放,Rt△ABD中∠D所对直角边与Rt△ACB斜边恰好重合.以AB为直径的圆经过点C,且与AD交于点 E,分别连接EB,EC.

(1)求证:EC平分∠AEB;
(2)求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=kx+b与反比例函数y=
 (x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.
(x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.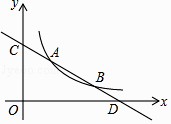
(1)求直线AB的解析式;
(2)若点P是x轴上一动点,当△COD与△ADP相似时,求点P的坐标.
相关试题

