搜索
【题目】如图，在△ABC中，∠C=90，AC=12cm，BC=24cm，动点P从点A开始沿边AC向点C以2cm/s的速度移动．动点Q从点B开始沿边BC向点C以4cm/s的速度移动，如果P、Q分别从点A、B同时出发，那么△PCQ的面积S随出发时间t如何变化？（写出函数关系式及t的取值范围）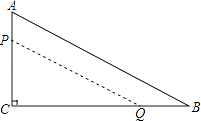 
参考答案：
【答案】解：∵动点P从点A开始沿边AC向点C以2cm/s的速度移动．动点Q从点B开始沿边BC向点C以4cm/s的速度移动，
∴设t秒时，△PCQ的面积为S，根据题意得出：
S= 
CQ×PC= （24﹣4t）×（12﹣2t）=4（6﹣t）2（0≤t≤6）
【解析】根据两点移动速度以及移动方向得出CQ以及PC的长，进而得出S与t的函数关系式．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，过点B（6，0）的直线AB与直线OA相交于点A（4，2），与y轴相交于点C，动点M在线段OA和射线AC上运动．
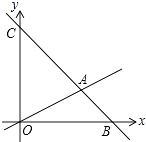
（1）求直线AB的解析式；
（2）若△OMC的面积是△OAC的面积的
，请直接写出此时点M的坐标 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图甲是一个长为2m，宽为2n的长方形，沿图中的虚线剪成四个全等的小长方形，再按图乙围成一个较大的正方形．
（1）请用两种方法表示图中阴影部分面积（只需表示，不必化简）；
（2）比较（1）两种结果，你能得到怎样的等量关系？
请你用（2）中得到等量关系解决下面问题：如果m﹣n=5，mn=14，求m+n的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校学生会向全校1900名学生发起了爱心捐款活动，为了解捐款情况，学生会随机调查了部分学生的捐款金额，并用得到的数据绘制了如下统计图1和图2，请根据相关信息，解答系列问题：
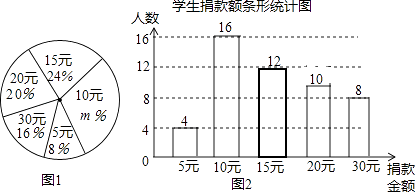
（1）本次接受随机抽样调查的学生人数为人，图1中m的值是 ．
（2）求本次调查获取的样本数据的平均数、众数和中位数；
（3）根据样本数据，估计该校本次活动捐款金额为10元的学生人数． -
科目： 来源： 题型：
查看答案和解析>>【题目】图①是一个长为2m，宽为2n的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后按图②的形状拼成一个正方形．
（1）图②中的阴影部分的面积为________；
（2）观察图②，三个代数式（m+n）2 ， （m﹣n）2 ， mn之间的等量关系是________；
（3）观察图③，你能得到怎样的代数等式呢？
（4）试画出一个几何图形，使它的面积能表示（m+n）（m+3n）；
（5）若x+y=﹣6，xy=2.75，求x﹣y的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线AB，CD，EF相交于点O，则∠AOD的对顶角是_________，∠AOC的邻补角是_______．若∠AOC＝50°，则∠BOD＝__________，∠COB＝______________．
-
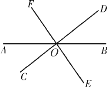
科目： 来源： 题型：
查看答案和解析>>【题目】一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为x h，两车之间的距离为y km，如图所示的折线表示y与x之间的函数关系．根据图象进行以下探究：
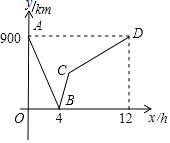
（1）甲、乙两地之间的距离为km；
（2）请解释图中点B的实际意义；
（3）求慢车和快车的速度；
（4）求线段BC所表示的y与x之间的函数关系式，并写出自变量x的取值范围．
相关试题
