【题目】已知射线AB∥射线CD,P为一动点,AE平分∠PAB,CE平分∠PCD,且AE与CE相交于点E.

(1)在图1中,当点P运动到线段AC上时,∠APC=180°.
①直接写出∠AEC的度数;②求证:∠AEC=∠EAB+∠ECD;
(2)当点P运动到图2的位置时,猜想∠AEC与∠APC之间的关系,并加以说明;
(3)当点P运动到图3的位置时,(2)中的结论是否还成立?若成立,请说明理由;若不成立,请写出∠AEC与∠APC之间的关系,并加以证明。
参考答案:
【答案】(1))①∠AEC=90°②见解析;(2)∠AEC=![]() ∠APC, 理由见解析;(3)不成立,∠AEC=180
∠APC, 理由见解析;(3)不成立,∠AEC=180![]() ∠APC ,理由见解析
∠APC ,理由见解析
【解析】
(1)①由平行线的性质可得出∠PAB+∠PCD=180°,进而可得出∠AEC的度数;
②在图1中,过E作EF∥AB,根据平行线的性质可得出∠AEF=∠EAB、∠CEF=∠ECD,进而即可证出∠AEC=∠AEF+∠CEF=∠EAB+∠ECD;
(2)猜想:∠AEC=![]() ∠APC,由角平分线的定义可得出∠EAB=
∠APC,由角平分线的定义可得出∠EAB=![]() ∠PAB、∠ECD=
∠PAB、∠ECD=![]() ∠PCD,由(1)可知∠AEC=∠EAB+∠ECD、∠APC=∠PAB+∠PCD,进而即可得出∠AEC=
∠PCD,由(1)可知∠AEC=∠EAB+∠ECD、∠APC=∠PAB+∠PCD,进而即可得出∠AEC=![]() (∠PAB+∠PCD)=
(∠PAB+∠PCD)=![]() ∠APC;
∠APC;
(3)在图3中,(2)中的结论不成立,而是满足∠AEC=180°-![]() ∠APC,过P作PQ∥AB,由平行线的性质可得出∠PAB+∠APQ=180°、∠CPQ+∠PCD=180°,进而可得出∠PAB+∠PCD=360°-∠APC,再由角平分线的定义可得出∠EAB=
∠APC,过P作PQ∥AB,由平行线的性质可得出∠PAB+∠APQ=180°、∠CPQ+∠PCD=180°,进而可得出∠PAB+∠PCD=360°-∠APC,再由角平分线的定义可得出∠EAB=![]() ∠PAB、∠ECD=
∠PAB、∠ECD=![]() ∠PCD,结合(1)的结论即可证出∠AEC=180°-
∠PCD,结合(1)的结论即可证出∠AEC=180°-![]() ∠APC.
∠APC.
(1)①∵AB∥CD,
∴∠PAB+∠PCD=180°,
∴∠AEC=90°;
②证明:在图1中,过E作EF∥AB,则∠AEF=∠EAB.
∵AB∥CD,
∴EF∥CD,
∴∠CEF=∠ECD.
∴∠AEC=∠AEF+∠CEF=∠EAB+∠ECD.
(2)猜想:∠AEC=![]() ∠APC,理由如下:
∠APC,理由如下:
∵AE、CE分别平分∠PAB和∠PCD,
∴∠EAB=![]() ∠PAB,∠ECD=
∠PAB,∠ECD=![]() ∠PCD.
∠PCD.
由(1)知∠AEC=∠EAB+∠ECD,∠APC=∠PAB+∠PCD,
∴∠AEC=![]() ∠PAB+
∠PAB+![]() ∠PCD=
∠PCD=![]() (∠PAB+∠PCD)=
(∠PAB+∠PCD)= ![]() ∠APC.
∠APC.
(3)在图3中,(2)中的结论不成立,而是满足∠AEC=180![]() ∠APC,
∠APC,

其证明过程是:
过P作PQ∥AB,则∠PAB+∠APQ=180°.
∵AB∥CD,
∴PQ∥CD,
∴∠CPQ+∠PCD=180.
∴∠PAB+∠APQ+∠CPQ+∠PCD=360°,即∠PAB+∠PCD=360°∠APC.
∵AE、CE分别平分∠PAB和∠PCD,
∴∠EAB=![]() ∠PAB,∠ECD=
∠PAB,∠ECD=![]() ∠PCD.
∠PCD.
由(1)知∠AEC=∠EAB+∠ECD,
∴∠AEC=![]() ∠PAB+
∠PAB+![]() ∠PCD=
∠PCD=![]() (∠PAB+∠PCD)= 180°-
(∠PAB+∠PCD)= 180°-![]() ∠APC.
∠APC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,利用标杆
 测量建筑物的高度,标杆
测量建筑物的高度,标杆  高
高  ,测得
,测得 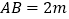 ,
,  ,则楼高
,则楼高  为=
为=  .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O与直线
 相离,圆心
相离,圆心 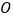 到直线
到直线  的距离
的距离  ,
,  ,将直线
,将直线  绕点
绕点  逆时针旋转
逆时针旋转  后得到的直线
后得到的直线  刚好与⊙O相切于点
刚好与⊙O相切于点  ,则⊙O的半径= .
,则⊙O的半径= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某高校共有5个大餐厅和2个小餐厅。经过测试:同时开放1个大餐厅和2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅和1个小餐厅,可供2280名学生就餐。
(1)1个大餐厅和1个小餐厅分别可供多少名学生就餐?
(2)若7个餐厅同时开放,能否供全校的5300名学生就餐?请说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是OB的反向延长线.

(1)射线OC的方向是 ;
(2)若射线OE平分∠COD,求∠AOE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于
 的方程
的方程  没有实数根,则二次函数
没有实数根,则二次函数 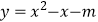 的图象的顶点在第象限.
的图象的顶点在第象限. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=60°,BD、CD分别平分∠ABC、∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、∠BCN,BF、CF分别平分∠EBC、∠ECQ,则∠F=________.

相关试题

