【题目】某公司经营杨梅业务,以3万元/吨的价格向农户收购杨梅后,分拣成A、B两类,A类杨梅包装后直接销售;B类杨梅深加工后再销售.A类杨梅的包装成本为1万元/吨,根据市场调查,它的平均销售价格y(单位:万元/吨)与销售数量x(x≥2)之间的函数关系如图;B类杨梅深加工总费用s(单位:万元)与加工数量t(单位:吨)之间的函数关系是s=12+3t,平均销售价格为9万元/吨. 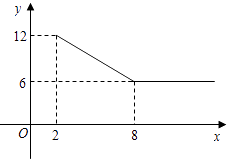
(1)直接写出A类杨梅平均销售价格y与销售量x之间的函数关系式;
(2)第一次,该公司收购了20吨杨梅,其中A类杨梅有x吨,经营这批杨梅所获得的毛利润为w万元(毛利润=销售总收入﹣经营总成本). ①求w关于x的函数关系式;
②若该公司获得了30万元毛利润,问:用于直销的A类杨梅有多少吨?
(3)第二次,该公司准备投入132万元资金,请设计一种经营方案,使公司获得最大毛利润,并求出最大毛利润.
参考答案:
【答案】
(1)解:①当2≤x<8时,如图,

设直线AB解析式为:y=kx+b,
将A(2,12)、B(8,6)代入得:
![]() ,解得
,解得 ![]() ,
,
∴y=﹣x+14;
②当x≥8时,y=6.
所以A类杨梅平均销售价格y与销售量x之间的函数关系式为:
y= ![]()
(2)解:设销售A类杨梅x吨,则销售B类杨梅(20﹣x)吨.
①当2≤x<8时,
wA=x(﹣x+14)﹣x=﹣x2+13x;
wB=9(20﹣x)﹣[12+3(20﹣x)]=108﹣6x
∴w=wA+wB﹣3×20
=(﹣x2+13x)+(108﹣6x)﹣60
=﹣x2+7x+48;
当x≥8时,
wA=6x﹣x=5x;
wB=9(20﹣x)﹣[12+3(20﹣x)]=108﹣6x
∴w=wA+wB﹣3×20
=(5x)+(108﹣6x)﹣60
=﹣x+48.
∴w关于x的函数关系式为:
w= ![]() .
.
②当2≤x<8时,﹣x2+7x+48=30,解得x1=9,x2=﹣2,均不合题意;
当x≥8时,﹣x+48=30,解得x=18.
∴当毛利润达到30万元时,直接销售的A类杨梅有18吨
(3)解:设该公司用132万元共购买了m吨杨梅,其中A类杨梅为x吨,B类杨梅为(m﹣x)吨,
则购买费用为3m万元,A类杨梅加工成本为x万元,B类杨梅加工成本为[12+3(m﹣x)]万元,
∴3m+x+[12+3(m﹣x)]=132,化简得:x=3m﹣60.
①当2≤x<8时,
wA=x(﹣x+14)﹣x=﹣x2+13x;
wB=9(m﹣x)﹣[12+3(m﹣x)]=6m﹣6x﹣12
∴w=wA+wB﹣3×m
=(﹣x2+13x)+(6m﹣6x﹣12)﹣3m
=﹣x2+7x+3m﹣12.
将3m=x+60代入得:w=﹣x2+8x+48=﹣(x﹣4)2+64
∴当x=4时,有最大毛利润64万元,
此时m= ![]() ,m﹣x=
,m﹣x= ![]() ;
;
②当x≥8时,
wA=6x﹣x=5x;
wB=9(m﹣x)﹣[12+3(m﹣x)]=6m﹣6x﹣12
∴w=wA+wB﹣3×m
=(5x)+(6m﹣6x﹣12)﹣3m
=﹣x+3m﹣12.
将3m=x+60代入得:w=48
∴当x>8时,有最大毛利润48万元.
综上所述,购买杨梅共 ![]() 吨,其中A类杨梅4吨,B类
吨,其中A类杨梅4吨,B类 ![]() 吨,公司能够获得最大毛利润,最大毛利润为64万元.
吨,公司能够获得最大毛利润,最大毛利润为64万元.
【解析】(1)这是一个分段函数,分别求出其函数关系式;(2)①当2≤x<8时及当x≥8时,分别求出w关于x的表达式.注意w=销售总收入﹣经营总成本=wA+wB﹣3×20;②若该公司获得了30万元毛利润,将30万元代入①中求得的表达式,求出A类杨梅的数量;(3)本问是方案设计问题,总投入为132万元,这笔132万元包括购买杨梅的费用+A类杨梅加工成本+B类杨梅加工成本.共购买了m吨杨梅,其中A类杨梅为x吨,B类杨梅为(m﹣x)吨,分别求出当2≤x<8时及当x≥8时w关于x的表达式,并分别求出其最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=
 ,当x=2时,y=3.
,当x=2时,y=3.
(1)求m的值;
(2)当3≤x≤6时,求函数值y的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某翼装飞行员从离水平地面高AC=500m的A处出发,沿着俯角为15°的方向,直线滑行1600米到达D点,然后打开降落伞以75°的俯角降落到地面上的B点.求他飞行的水平距离BC(结果精确到1m).
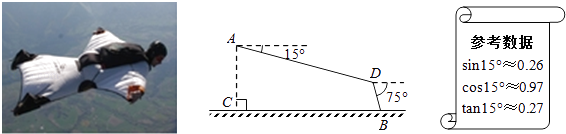
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了估计鱼塘中成品鱼(个体质量在0.5kg及以上,下同)的总质量,先从鱼塘中捕捞50条成品鱼,称得它们的质量如表:
质量/kg
0.5
0.6
0.7
1.0
1.2
1.6
1.9
数量/条
1
8
15
18
5
1
2
然后做上记号再放回水库中,过几天又捕捞了100条成品鱼,发现其中2条带有记号.
(1)请根据表中数据补全如图的直方图(各组中数据包括左端点不包括右端点).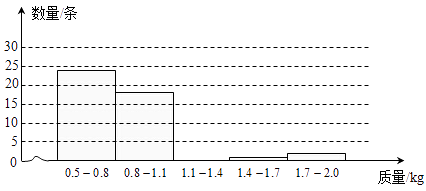
(2)根据图中数据分组,估计从鱼塘中随机捕一条成品鱼,其质量落在哪一组的可能性最大?
(3)根据图中数据分组,估计鱼塘里质量中等的成品鱼,其质量落在哪一组内?
(4)请你用适当的方法估计鱼塘中成品鱼的总质量(精确到1kg). -
科目: 来源: 题型:
查看答案和解析>>【题目】研究几何图形,我们往往先给出这类图形的定义,再研究它的性质和判定. 定义:六个内角相等的六边形叫等角六边形.
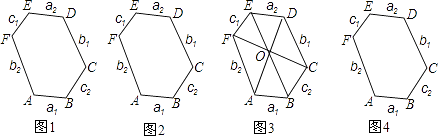
(1)研究性质 ①如图1,等角六边形ABCDEF中,三组正对边AB与DE,BC与EF,CD与AF分别有什么位置关系?证明你的结论.
②如图2,等角六边形ABCDEF中,如果有AB=DE,则其余两组正对边BC与EF,CD与AF相等吗?证明你的结论.
③如图3,等角六边形ABCDEF中,如果三条正对角线AD,BE,CF相交于一点O,那么三组正对边AB与DE,BC与EF,CD与AF分别有什么数量关系?证明你的结论.
(2)探索判定 三组正对边分别平行的六边形,至少需要几个内角为120°,才能保证六边形一定是等角六边形? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,汽车在东西向的公路l上行驶,途中A,B,C,D四个十字路口都有红绿灯.AB之间的距离为800米,BC为1000米,CD为1400米,且l上各路口的红绿灯设置为:同时亮红灯或同时亮绿灯,每次红(绿)灯亮的时间相同,红灯亮的时间与绿灯亮的时间也相同.若绿灯刚亮时,甲汽车从A路口以每小时30千米的速度沿l向东行驶,同时乙汽车从D路口以相同的速度沿l向西行驶,这两辆汽车通过四个路口时都没有遇到红灯,则每次绿灯亮的时间可能设置为( )
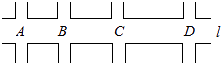
A.50秒
B.45秒
C.40秒
D.35秒 -
科目: 来源: 题型:
查看答案和解析>>【题目】把球放在长方体纸盒内,球的一部分露出盒外,其主视图如图.⊙O与矩形ABCD的边BC,AD分别相切和相交(E,F是交点),已知EF=CD=8,则⊙O的半径为 .

相关试题

