【题目】如图,在矩形ABCD中,点E为边AB上一点,且AE=![]() AB,EF⊥EC,连接BF.
AB,EF⊥EC,连接BF.
(1)求证:△AEF∽△BCE;
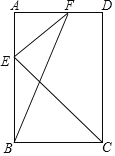
(2)若AB=3![]() ,BC=3,求线段FB的长.
,BC=3,求线段FB的长.
参考答案:
【答案】(1)证明见解析(2)![]()
【解析】分析:(1)、根据矩形的性质以及EF⊥EC得出∠AFE=∠BEC,从而得出三角形相似;(2)、根据题意得出AE和BE的长度,然后根据三角形相似得出AF的长度,然后根据Rt△ABF的勾股定理得出答案.
详解:(1)∵四边形ABCD是矩形, ∴∠A=∠CBE=90°, ∴∠AEF+∠AFE=90°,
又∵EF⊥EC, ∴∠AEF+∠BEC=90°, ∴∠AFE=∠BEC, ∴△AEF∽△BCE;
(2)∵AB=3![]() 、AE=
、AE=![]() AB, ∴AE=
AB, ∴AE=![]() 、BE=2
、BE=2![]() , ∵△AEF∽△BCE,
, ∵△AEF∽△BCE,
∴![]() =
=![]() ,即
,即![]() =
=![]() , 解得:AF=2, 则BF=
, 解得:AF=2, 则BF=![]() =
=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某报社为了了解市民“获取新闻的最主要途径”,开展了一次抽样调查,根据调查结果绘制了如下三种不完整的统计图表.
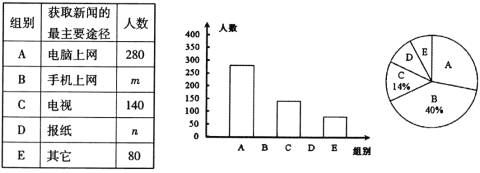
请根据图表信息解答下列问题:
(1)统计表中的
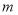 = ,
= ,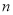 = ,并请补全条形统计图;
= ,并请补全条形统计图;(2)扇形统计图中“
 ”所对应的圆心角的度数是 ;
”所对应的圆心角的度数是 ;(3)若该市约有100万人,请你估计其中将“电脑上网”和“手机上网”作为“获取新闻的最主要途径”的总人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一辆摩拜单车放在水平的地面上,车把头下方A处与坐垫下方B处在平行于地面的水平线上,A、B之间的距离约为49cm,现测得AC、BC与AB的夹角分别为45°与68°,若点C到地面的距离CD为28cm,坐垫中轴E处与点B的距离BE为4cm,求点E到地面的距离(结果保留一位小数).(参考数据:sin68°≈0.93,cos68°≈0.37,cot68°≈0.40)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=4﹣x与反比例函数y=
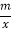 (m>0,x>0)的图象交于A,B两点,且点A的横坐标为1,与x轴,y轴分别相交于C,D两点.
(m>0,x>0)的图象交于A,B两点,且点A的横坐标为1,与x轴,y轴分别相交于C,D两点.(1)求另一个交点B的坐标;
(2)利用函数图象求关于x的不等式4﹣x<
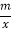 的解集;
的解集;(3)求三角形AOB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,PB与⊙O相切于点B,过点B作OP的垂线BA,垂足为C,交⊙O于点A,连结PA,AO,AO的延长线交⊙O于点E,与PB的延长线交于点D.
(1)求证:PA是⊙O的切线;
(2)若tan∠BAD=
 ,且OC=4,求BD的长.
,且OC=4,求BD的长.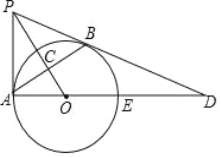
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,给出如下定义:对于点P(m,n),若点Q(2﹣m,n﹣1),则称点Q为点P的“δ点”.例如:点(﹣2,5)的“δ点”坐标为(4,4).
(1)某点的“δ点”的坐标是(﹣1,3),则这个点的坐标为 ;
(2)若点A的坐标是(2﹣m,n﹣1),点A的“δ点”为A1点,点A1的“δ点”为A2点,点A2的“δ点”为A3点,…,点A1的坐标是 ;点A2015的坐标是 ;
(3)函数y=﹣x2+2x(x≤1)的图象为G,图象G上所有点的“δ点”构成图象H,图象G与图象H的组合图形记为“图形Ю”,当点(p,q)在“图形Ю”上移动时,若k≤p≤1+2
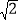 ,﹣8≤q≤1,求k的取值范围
,﹣8≤q≤1,求k的取值范围 -
科目: 来源: 题型:
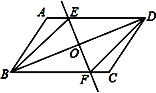
查看答案和解析>>【题目】已知:如图,在平行四边形ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
(1)求证:△DOE≌△BOF.
(2)当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由.
相关试题

