【题目】如图,直线y=-2x+6与x轴交于点A,与直线y=x交于点B.
(1)点A坐标为_____________.
(2)动点M从原点O出发,以每秒1个单位长度的速度沿着O→A的路线向终点A匀速运动,过点M作MP⊥x轴交直线y=x于点P,然后以MP为直角边向右作等腰直角△MPN.设运动t秒时,ΔMPN与ΔOAB重叠部分的面积为S.求S与t之间的函数关系式,并直接写出t的取值范围.

参考答案:
【答案】(1)(3,0);(2)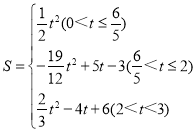
【解析】
(1)将y=0代入y=-2x+6可得x=3,即可得出点A坐标;
(2)分点N在直线AB左侧时,点N在直线AB右侧且P在直线AB左侧时,以及点P在直线AB右侧三种情况讨论,利用数形结合的思想,根据重叠部分的形状,分别用含t的式子表示出三角形的底边和高,从而得到重叠部分的面积.
(1) 将y=0代入y=-2x+6可得x=3,
所以点A坐标为(3,0)
故答案为:(3,0)
(2)如图一,
由![]() 得
得![]()

∴B(2,2)
过点B作BH⊥x轴于点H
∴BH=OH=2,∠AOB=45°
∵PM⊥x轴
∴OM=MP=t
∵等腰直角ΔMPN
∴PN∥x轴
∴∠N=∠NMA=45°
∴∠AOB=∠NMA=45°
∴MN∥OB
∴设直线MN为y=x+b
∵OM=t
∴y=x-t
当点N在直线y=-2x+6上时,OM=PM=PN=t,
∴N(2t,t)
∴t=-2×2t+6,解得:t=![]()
∴当![]() 时,
时,![]()
如图二,当点P在直线y=-2x+6上时,OM=PM=t,
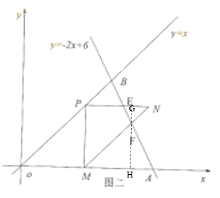
可得t=-2t+6,解得:t=2
当![]() 时,PN与AB交于点E,MN与AB交于点F,
时,PN与AB交于点E,MN与AB交于点F,
∵P(t,t)
∴t=-2x+6
∴![]()
∴![]()
∴![]()
∴![]()
∵OA=3
∴MA=3-t
由![]()
得F(2+![]() t,2-
t,2-![]() t)
t)
过点F作△ENF的高GF, △FMA的高HF
∴HF=2-![]() t
t
∴![]()
∴![]()
∴![]() ;
;
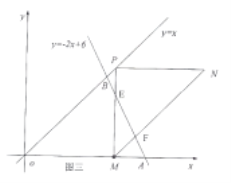
如图三,当M与A重合时,t=3
故当![]() 时,PM与AB交于点E,MN与AB交于点F,有E(t, -2t+6),F(2+
时,PM与AB交于点E,MN与AB交于点F,有E(t, -2t+6),F(2+![]() t,2-
t,2-![]() t),
t),
∴![]() ,
,
∴![]() ;
;
综上所述,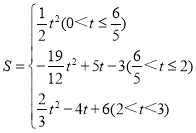 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲骑自行年,乙乘坐汽车从A地出发沿同一路线匀速前往B地,甲先出发.设甲行驶的时间为x(h),甲、乙两人距出发点的路程S甲(km)、S乙(km)关于x的函数图象如图1所示,甲、乙两人之同的距离y(km)关于x的函数图象如图2所示,请你解决以下问题:
(1)甲的速度是__________km/h,乙的速度是_______km/h;
(2)a=_______,b=_______;
(3)甲出发多少时间后,甲、乙两人第二次相距7.5km?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABD中,AB=AD,将△ABD沿BD对折,使点A翻折到点C,E是BD上一点。且BE>DE,连接AE并延长交CD于F,连接CE.
(1)依题意补全图形;
(2)判断∠AFD与∠BCE的大小关系并加以证明;
(3)若∠BAD=120°,过点A作∠FAG=60°交边BC于点G,若BG=m,DF=n,求AB的长度(用含m,n的代数式表示).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.
(1)求证:△DCE≌△BFE;
(2)若CD=2,∠ADB=30°,求BE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:数学课上,老师出示了这祥一个问题:
如图,在正方形ABCD中,点F在AB上,点E在BC延长线上。且AF=CE,连接EF,过点D作DH⊥FE于点H,连接CH并延长交BD于点0,∠BFE=75°.求
 的值.某学习小组的同学经过思考,交流了自己的想法:
的值.某学习小组的同学经过思考,交流了自己的想法:小柏:“通过观察和度量,发现点H是线段EF的中点”。
小吉:“∠BFE=75°,说明图形中隐含着特殊角”;
小亮:“通过观察和度量,发现CO⊥BD”;
小刚:“题目中的条件是连接CH并延长交BD于点O,所以CO平分∠BCD不是己知条件。不能由三线合一得到CO⊥BD”;
小杰:“利用中点作辅助线,直接或通过三角形全等,就能证出CO⊥BD,从而得到结论”;……;
老师:“延长DH交BC于点G,若刪除∠BFB=75°,保留原题其余条件,取AD中点M,连接MH,如果给出AB,MH的值。那么可以求出GE的长度”.
请回答:(1)证明FH=EH;
(2)求
 的值;
的值;(3)若AB=4.MH=
 ,则GE的长度为_____________.
,则GE的长度为_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于给定的两个“函数,任取自变量x的一个值,当x<1时,它们对应的函数值互为相反数;当x≥1时,它们对应的函数值相等,我们称这样的两个函数互为相关函数.例如:一次函数y=x-4,它的相关函数为
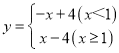 .
.(1)一次函数y= -x+5的相关函数为______________.
(2)已知点A(b-1,4),点B坐标(b+3,4),函数y=3x-2的相关函数与线段AB有且只有一个交点,求b的取值范围.
(3)当b+1≤x≤b+2时,函数y=-3x+b-2的相关函数的最小值为3,求b的值.
相关试题

