【题目】如图,AB为⊙O的直径,点C为⊙O上一点,将弧BC沿直线BC翻折,使弧BC的中点D恰好与圆心O重合,连接OC,CD,BD,过点C的切线与线段BA的延长线交于点P,连接AD,在PB的另一侧作∠MPB=∠ADC.
(1)判断PM与⊙O的位置关系,并说明理由;
(2)若PC=![]() ,求四边形OCDB的面积.
,求四边形OCDB的面积.

参考答案:
【答案】(1)PM与⊙O相切,理由见解析;(2)![]() .
.
【解析】
(1)连接DO并延长交PM于E,如图,利用折叠的性质得OC=DC,BO=BD,则可判断四边形OBDC为菱形,所以OD⊥BC,△OCD和△OBD都是等边三角形,从而计算出∠COP=∠EOP=60°,接着证明PM∥BC得到OE⊥PM,所以OE=![]() OP,根据切线的性质得到OC⊥PC,则OC=
OP,根据切线的性质得到OC⊥PC,则OC=![]() OP,从而可判定PM是⊙O的切线;
OP,从而可判定PM是⊙O的切线;
(2)先在Rt△OPC中计算出OC=1,然后根据等边三角形的面积公式计算四边形OCDB的面积.
(1)PM与⊙O相切.
理由如下:连接DO并延长交PM于E,如图,
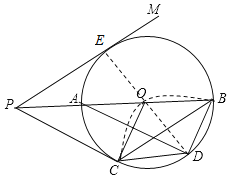
∵弧BC沿直线BC翻折,使弧BC的中点D恰好与圆心O重合,
∴OC=DC,BO=BD,
∴OC=DC=BO=BD,
∴四边形OBDC为菱形,
∴OD⊥BC,
∴△OCD和△OBD都是等边三角形,
∴∠COD=∠BOD=60°,
∴∠COP=∠EOP=60°,
∵∠MPB=∠ADC,
而∠ADC=∠ABC,
∴∠ABC=∠MPB,
∴PM∥BC,
∴OE⊥PM,
∴OE=![]() OP,
OP,
∵PC为⊙O的切线,
∴OC⊥PC,
∴OC=![]() OP,
OP,
∴OE=OC,
而OE⊥PC,
∴PM是⊙O的切线;
(2)在Rt△OPC中,OC=![]() PC=
PC=![]() ,
,
∴四边形OCDB的面积=2S△OCD=2×![]() ×12=
×12=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读:多项式
 当
当 取某些实数时,
取某些实数时, 是完全平方式.
是完全平方式.例如:
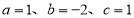 时,
时, , 发现:
, 发现:  ;
; 时,
时, ,发现:
,发现: ;
; 时,
时, , 发现:
, 发现: ;
;……
根据阅读解答以下问题:
 分解因式:
分解因式: 
 若多项式
若多项式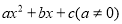 是完全平方式,则
是完全平方式,则 之间存在某种关系,用等式表示
之间存在某种关系,用等式表示 之间的关系:
之间的关系:  在实数范围内,若关于
在实数范围内,若关于 的多项式
的多项式 是完全平方式,求
是完全平方式,求 值.
值. 求多项式:
求多项式: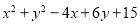 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,李老师准备了四张背面看上去无差别的卡片A,B,C,D,每张卡片的正面标有字母a,b,c表示三条线段(如图),把四张卡片背面朝上放在桌面上,李老师从这四张卡片中随机抽取一张卡片后不放回,再随机抽取一张.

(1)用树状图或者列表表示所有可能出现的结果;
(2)求抽取的两张卡片中每张卡片上的三条线段都能组成三角形的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD为∠BAC的平分线,添下列条件后,不能证明△ABD≌△ACD的是( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 中,
中, ,在
,在 、
、 上分别找一点
上分别找一点 ,使
,使 周长最小时,则
周长最小时,则 的度数为( )
的度数为( )
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AC,EB=EC,AE的延长线交BC于D,则图中全等的三角形共有_____对.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC 中,BD、CE分别是AC、AB上的高,BD与CE交于点O.BD=CE

(1)问△ABC为等腰三角形吗?为什么?
(2)问点O在∠A的平分线上吗?为什么?
相关试题

