【题目】在△ABC中,D是BC的中点,且AD=AC,DE⊥BC,与AB相交于点E,EC与AD相交于点F.
(1)求证:△ABC∽△FCD;
(2)若DE=3,BC=8,求△FCD的面积.
参考答案:
【答案】
(1)证明:∵D是BC的中点,DE⊥BC,
∴BE=CE,
∴∠B=∠DCF,
∵AD=AC,
∴∠FDC=∠ACB,
∴△ABC∽△FCD.
(2)解:过A作AG⊥CD,垂足为G.
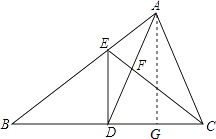
∵AD=AC,
∴DG=CG,
∴BD:BG=2:3,
∵ED⊥BC,
∴ED∥AG,
∴△BDE∽△BGA,
∴ED:AG=BD:BG=2:3,
∵DE=3,
∴AG= ![]() ,
,
∵△ABC∽△FCD,BC=2CD,
∴ ![]() =(
=( ![]() )2=
)2= ![]() .
.
∵S△ABC= ![]() ×BC×AG=
×BC×AG= ![]() ×8×
×8× ![]() =18,
=18,
∴S△FCD= ![]() S△ABC=
S△ABC= ![]() .
.
【解析】(1)先证明∠B=∠DCF和∠FDC=∠ACB,可证得△ABC∽△FCD;
(2)过A作AG⊥CD,垂足为G.先证明△BDE∽△BGA,再由相似三角形的性质求得AG的长,由(1)知△ABC∽△FCD,利用面积比等于相似比的平方可求得△ABC的面积,进而可求得△FCD的面积.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题【再现】如图①,在△ABC中,点D,E分别是AB,AC的中点,可以得到:DE∥BC,且DE=
 BC.(不需要证明)
BC.(不需要证明)
(1)【探究】如图②,在四边形ABCD中,点E,F,G,H分别是AB,BC,CD,DA的中点,判断四边形EFGH的形状,并加以证明.
(2)【应用】在(1)【探究】的条件下,四边形ABCD中,满足什么条件时,四边形EFGH是菱形?你添加的条件是: . (只添加一个条件)
(3)如图③,在四边形ABCD中,点E,F,G,H分别是AB,BC,CD,DA的中点,对角线AC,BD相交于点O.若AO=OC,四边形ABCD面积为5,则阴影部分图形的面积和为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中∠A=30°,E是AC边上的点,先将△ABE沿着BE翻折,翻折后△ABE的AB边交AC于点D,又将△BCD沿着BD翻折,C点恰好落在BE上,此时∠CDB=80°,则原三角形的∠B为 _____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在Rt△ABC中,∠C=90°,AB=10,BC=6,点P从点A出发,沿折线AB﹣BC向终点C运动,在AB上以每秒5个单位长度的速度运动,在BC上以每秒3个单位长度的速度运动,点Q从点C出发,沿CA方向以每秒
 个单位长度的速度运动,P,Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.
个单位长度的速度运动,P,Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.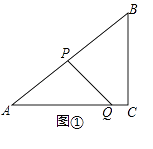
(1)求线段AQ的长;(用含t的代数式表示)
(2)连结PQ,当PQ与△ABC的一边平行时,求t的值;
(3)如图②,过点P作PE⊥AC于点E,以PE,EQ为邻边作矩形PEQF,点D为AC的中点,连结DF.设矩形PEQF与△ABC重叠部分图形的面积为S.①当点Q在线段CD上运动时,求S与t之间的函数关系式;②直接写出DF将矩形PEQF分成两部分的面积比为1:2时t的值.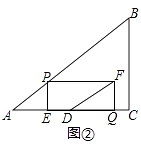
-
科目: 来源: 题型:
查看答案和解析>>【题目】画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
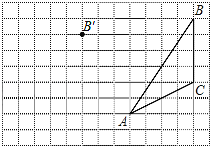
(1)在给定方格纸中画出平移后的△A′B′C′;
(2)画出AB边上的中线CD和BC边上的高线AE;
(3)线段AA′与线段BB′的关系是: ;
(4)求△A′B′C′的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )

A. BD=CE B. AD=AE C. DA=DE D. BE=CD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB//DG, AD∥EF,
(1)试说明:
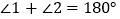 ;
;(2) 若DG是∠ADC的平分线,
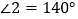 ,求∠B的度数.
,求∠B的度数.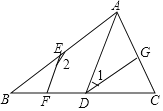
相关试题

