Question

【题目】已知∠A为锐角,

证明:(1)sin A=cos (90°-∠A);

(2)sin2 A+cos2 A=1;

(3)tan A=.

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）证明见解析.

【解析】试题分析：

如图，把∠A放到Rt△ABC（∠C=90°）中去，利用“锐角三角函数的定义”可得：，利用这些式子结合“勾股定理”和

“∠A+∠B=90°”就可证得这些等式是成立的.

试题解析：

作Rt△ABC,使∠C=90°,如图,

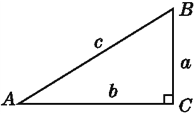
则sin A=，cos A= ，tan A=.

(1)∵cos B=，sin A=，

∴ sin A=cos B.

又∵∠A+∠B=90°，

∴∠B=90°-∠A,

∴sin A=cos (90°-∠A).

(2)∵sin A=，cos A=，且a2+b2=c2，

∴ sin2A+cos2A=+===1.

(3)∵sin A=，cos A=，

∴ ==.

又∵tan A=，

∴tan A=.