【题目】已知,如图,在△ABC中,∠A=∠ABC,直线EF分别交△ABC的边AB,AC和CB的延长线于点D,E,F.

(1)求证:∠F+∠FEC=2∠A;
(2)过B点作BM∥AC交FD于点M,试探究∠MBC与∠F+∠FEC的数量关系,并证明你的结论.
参考答案:
【答案】(1)证明见解析(2)∠MBC=∠F+∠FEC,证明见解析
【解析】试题分析:(1)根据三角形外角的性质,可得出∠FEC=∠A+∠ADE,∠F+∠BDF=∠ABC,再根据∠A=∠ABC,即可得出答案;
(2)由BM∥AC,得出∠MBA=∠A,∠A=∠ABC,得出∠MBC=∠MBA+∠ABC=2∠A,结合(1)的结论证得答案即可.
(1)证明:∵∠FEC=∠A+∠ADE,∠F+∠BDF=∠ABC,
∴∠F+∠FEC=∠F+∠A+∠ADE,
∵∠ADE=∠BDF,
∴∠F+∠FEC=∠A+∠ABC,
∵∠A=∠ABC,
∴∠F+∠FEC=∠A+∠ABC=2∠A.
(2)∠MBC=∠F+∠FEC.
证明:∵BM∥AC,
∴∠MBA=∠A,、
∵∠A=∠ABC,
∴∠MBC=∠MBA+∠ABC=2∠A,
又∵∠F+∠FEC=2∠A,
∴∠MBC=∠F+∠FEC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:5(3a2b﹣ab2﹣1)﹣(ab2+3a2b﹣5),其中a=1,b=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算﹣3a2b﹣2a2b的正确结果是( )
A.﹣1
B.﹣a2b
C.﹣5a2b
D.﹣5 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.
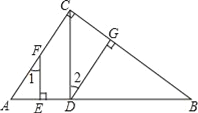
证明:∵DG⊥BC,AC⊥BC,(已知)
∴DG∥AC( )
∴∠2= ( )
∵∠1=∠2(已知)
∴∠1=∠DCA(等量代换)
∴EF∥CD( )
∴∠AEF=∠ADC( )
∵EF⊥AB(已知)
∴∠AEF=90°( )
∴∠ADC=90°(等量代换)
∴CD⊥AB(垂直定义)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a与b互为相反数,c、d互为倒数,|m|=2,计算2m﹣(a+b)2﹣(cd)3的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,点D为BC的中点,点E,F分别在直线AB,AC上运动,且始终保持AE=CF.
(1)如图①,若点E,F分别在线段AB,AC上,求证:DE=DF且DE⊥DF;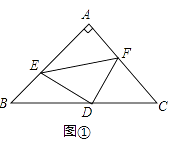
(2)如图②,若点E、F分别在线段AB,CA的延长线上,(1)中的结论是否依然成立?说明理由.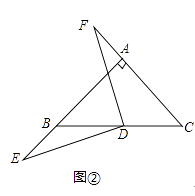
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以M,N为圆心,大于
 MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC:S△ABC=
1:3.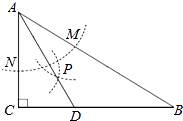
A.1
B.2
C.3
D.4
相关试题

