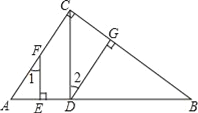
【题目】已知,如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.
证明:∵DG⊥BC,AC⊥BC,(已知)
∴DG∥AC( )
∴∠2= ( )
∵∠1=∠2(已知)
∴∠1=∠DCA(等量代换)
∴EF∥CD( )
∴∠AEF=∠ADC( )
∵EF⊥AB(已知)
∴∠AEF=90°( )
∴∠ADC=90°(等量代换)
∴CD⊥AB(垂直定义)
参考答案:
【答案】同位角相等,两直线平行;∠ACD; 两直线平行,内错角相等;同位角相等,两直线平行;两直线平行,同位角相等;垂直定义.
【解析】试题分析:已知DG⊥BC,AC⊥BC,根据垂直于同一条直线的两直线平行可得DG∥AC,由两直线平行,内错角相等可得∠2=∠ACD,已知∠1=∠2,等量代换得∠1=∠DCA,由同位角相等,两直线平行可得EF∥CD,由两直线平行,同位角相等可得∠AEF=∠ADC,已知EF⊥AB,由垂直定义可得∠AEF=90°,等量代换得∠ADC=90°,由垂直定义得CD⊥AB.
试题解析:
证明:∵DG⊥BC,AC⊥BC(已知),
∴DG∥AC(垂直于同一条直线的两直线平行 ),
∴∠2=∠ACD ( 两直线平行,内错角相等 ),
∵∠1=∠2(已知),
∴∠1=∠DCA(等量代换),
∴EF∥CD(同位角相等,两直线平行),
∴∠AEF=∠ADC(两直线平行,同位角相等),
∵EF⊥AB(已知),
∴∠AEF=90°(垂直定义),
∴∠ADC=90°(等量代换),
∴CD⊥AB(垂直定义).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是某种植物的种子在相同条件下发芽率试验的结果.
种子个数
100
400
900
1500
2500
4000
发芽种子个数
92
352
818
1336
2251
3601
发芽种子频率
0. 92
0. 88
0. 91
0. 89
0. 90
0. 90
根据上表中的数据,可估计该植物的种子发芽的概率为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:5(3a2b﹣ab2﹣1)﹣(ab2+3a2b﹣5),其中a=1,b=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算﹣3a2b﹣2a2b的正确结果是( )
A.﹣1
B.﹣a2b
C.﹣5a2b
D.﹣5 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在△ABC中,∠A=∠ABC,直线EF分别交△ABC的边AB,AC和CB的延长线于点D,E,F.

(1)求证:∠F+∠FEC=2∠A;
(2)过B点作BM∥AC交FD于点M,试探究∠MBC与∠F+∠FEC的数量关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a与b互为相反数,c、d互为倒数,|m|=2,计算2m﹣(a+b)2﹣(cd)3的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,点D为BC的中点,点E,F分别在直线AB,AC上运动,且始终保持AE=CF.
(1)如图①,若点E,F分别在线段AB,AC上,求证:DE=DF且DE⊥DF;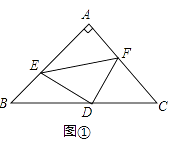
(2)如图②,若点E、F分别在线段AB,CA的延长线上,(1)中的结论是否依然成立?说明理由.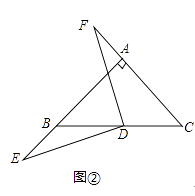
相关试题

