【题目】已知反比例函数![]() 的图象经过A(2,-4).
的图象经过A(2,-4).
(1)求k的值.
(2)这个函数的图象在哪几个象限?y随x的增大怎样变化?
(3)画出函数的图象.
(4)点B(-2,4),C(-1,5)在这个函数的图象上吗?
参考答案:
【答案】(1)k=9;(2)图象位于二、四象限,在每个象限内y随x的增大而增大;(3)见解析;(4)B(-2,4)在反比例函数的图象上,C(-1,5)不在反比例函数的图象上.
【解析】试题分析:(1)将已知点的坐标代入反比例函数的解析式即可求得k值;
(2)根据确定的k的符号判断其所在的象限和增减性;
(3)利用描点作图法作出图象即可;
(4)满足函数关系式即在,否则不在.
试题解析:解:(1)∵反比例函数![]() 的图象经过点A(2,﹣4),∴1﹣k=2×(﹣4)=﹣8;解得:k=9;
的图象经过点A(2,﹣4),∴1﹣k=2×(﹣4)=﹣8;解得:k=9;
(2)∵k=﹣8<0,∴图象位于二、四象限,在每个象限内y随x的增大而增大;
(3)图象为:
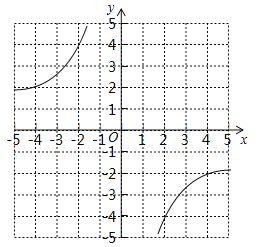
(4)∵﹣2×4=﹣8,﹣1×5=﹣5≠﹣8,∴B(﹣2,4)在反比例函数的图象上,C(﹣1,5)不在反比例函数的图象上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(0,a),B(b,a),且a、b满足(a﹣2)2+|b﹣4|=0,现同时将点A,B分别向下平移2个单位,再向左平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.

(1)求点C,D的坐标及四边形ABDC的面积S四边形ABCD;
(2)在y轴上是否存在一点M,连接MC,MD,使S△MCD=
 S四边形ABDC?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
S四边形ABDC?若存在这样一点,求出点M的坐标,若不存在,试说明理由;(3)点P是直线BD上的一个动点,连接PA,PO,当点P在BD上移动时(不与B,D重合),直接写出∠BAP、∠DOP、∠APO之间满足的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A的坐标是(﹣1,0),点B的坐标是(9,0),以AB为直径作⊙O′,交y轴的负半轴于点C,连接AC、BC,过A、B、C三点作抛物线.
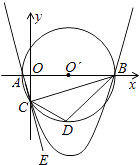
(1)求点C的坐标及抛物线的解析式;
(2)点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,求点D的坐标;并直接写出直线BC、直线BD的解析式;
(3)在(2)的条件下,抛物线上是否存在点P,使得∠PDB=∠CBD,若存在,请求出点P的坐标,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB,CD都垂直于x轴,垂足分别为B,D,若A(6,3),C(2,1), 则△OCD与四边形ABDC的面积比为( )
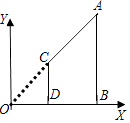
A.1:2
B.1:3
C.1:4
D.1:8 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线BC于点M,切点为N,则DM的长为( )

A.
B.
C.

D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】运用运算律计算:
(1)0.36+(-7.4)+0.3+(-0.6)+0.64;
(2)(-103)+(+1
 )+(-97)+(+100)+(-1
)+(-97)+(+100)+(-1 );
);(3)(-3
 )+(-2.16)+8
)+(-2.16)+8 +3
+3 +(-3.84)+(-0.25)+
+(-3.84)+(-0.25)+ ;
;(4)(-
 )+3
)+3 +|-0.75|+(-5
+|-0.75|+(-5 )+|-2
)+|-2 |.
|. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=k1x+b与双曲线y=
 相交于A(1,2)、B(m,-1)两点.
相交于A(1,2)、B(m,-1)两点.(1)求直线和双曲线的解析式;
(2)若A1(x1,y1)、A2(x2,y2)、A3(x3,y3)为双曲线上的三点,且x1<x2<0<x3,请直接写出y1、y2、y3的大小关系式;
(3)观察图象,请直接写出不等式k1x+b>
 的解集.
的解集.
相关试题

