搜索
【题目】设
，
是关于
的一元二次方程
的两实根，
的最小值是________．
参考答案：
【答案】
【解析】
设x1，x2是关于x的一元二次方程x2+2ax+a2+4a-2=0的两实根，首先：△=（2a）2-4（a2+4a-2）≥0可求得a≤，得到了关于a的取值范围．对要求值的式子化简：x12+x22=（x1+x2）2-2x1x2=2（a-2）2-4，设y=2（a-2）2-4，这是一个关于a的一元二次方程，其对称轴是a=2，开口方向向上．根据开口向上的二次函数的性质：距对称轴越近，其函数值越小．故在a≤的范围内，当a＝时，x12+x22的值最小；此时
+
＝2(2)24＝，即最小值为．
：∵△=（2a）2-4（a2+4a-2）≥0，∴a≤
又∵x1+x2=-2a，x1x2=a2+4a-2．
∴x12+x22=（x1+x2）2-2x1x2=2（a-2）2-4．
设y=2（a-2）2-4，根据二次函数的性质．
∵a≤
∴当a＝时，x12+x22的值最小．
此时 +＝2(2)24＝，即最小值为．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y＝－
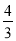x＋8与x轴、y轴分别交于点A和点B，M是OB的上的一点，若将△ABM沿M折叠，点B恰好落在x轴上的点B′处.（1）求A、B两点的坐标；
（2）求直线AM的表达式；
（3)在x轴上是否存在点P，使得以点P、M、B′为顶点的三角形是等腰二角形，若存在，请直接写出所有点P的坐标；若不存在，请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】（阅读理解）
截长补短法，是初中数学儿何题中一种输助线的添加方法，截长就是在长边上载取一条线段与某一短边相等，补短是通过在一条短边上延长一条线段与另一短边相等，从而解决问题.
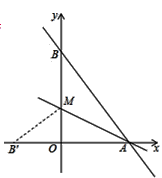
（1）如图1，△ABC是等边三角形，点D是边BC下方一点，∠BDC＝120°，探索线段DA、DB、DC之间的数量关系.
解题思路：延长DC到点E，使CE＝BD.连接AE，根据∠BAC＋∠BDC＝180°，可证∠ABD＝∠ACE,易证得△ABD≌△ACE，得出△ADE是等边三角形，所以AD＝DE，从而探寻线段DA、DB、DC之间的数量关系.
根据上述解题思路，请直接写出DA、DB、DC之间的数量关系是___________
（拓展延伸）
（2）如图2，在Rt△ABC中，∠BAC＝90°，AB＝AC.若点D是边BC下方一点，∠BDC＝90°，探索线段DA、DB、DC之间的数量关系，并说明理由;
（知识应用）
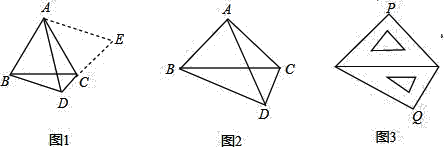
（3）如图3,一副三角尺斜边长都为14cm，把斜边重叠摆放在一起，则两块三角尺的直角项点之间的距离PQ的长为________cm.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点D在线段BC上，若BC＝DE，AC＝DC，AB＝EC，且∠ACE＝180°—∠ABC—2x°，则下列角中，大小为x°的角是
A.∠EFCB.∠ABCC.∠FDCD.∠DFC
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图：在
中，
，
，
，点
、
同时由
、
两点分别沿
、
方向向点
匀速移动，它们的速度都是
，设
秒后
的面积为面积的一半．则方程（一般形式）为：________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知锐角∠MPN，依照下列步骤进行尺规作图：
（1）在射线PN上截取线段PA；
（2）分别以P，A为圆心，大于
PA的长为半径作弧，两弧相交于E，F两点；（3）作直线EF，交射线PM于点B；
（4）在射线AN上截取AC＝PB；
（5）连接BC.
则∠BCP与∠MPN之间的数量关系是_______________________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，∠C＝90°，D是边BC上一点，连接AD，若∠BAD＋3∠CAD＝90°，DC＝a，BD＝b，则AB＝________. （用含a，b的式子表示）
相关试题
