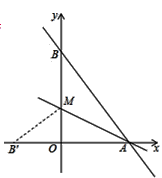
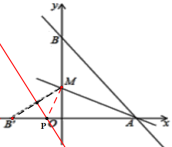
【题目】如图,直线y=-![]() x+8与x轴、y轴分别交于点A和点B,M是OB的上的一点,若将△ABM沿M折叠,点B恰好落在x轴上的点B′处.
x+8与x轴、y轴分别交于点A和点B,M是OB的上的一点,若将△ABM沿M折叠,点B恰好落在x轴上的点B′处.
(1)求A、B两点的坐标;
(2)求直线AM的表达式;
(3)在x轴上是否存在点P,使得以点P、M、B′为顶点的三角形是等腰二角形,若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)P(4,0)或
;(3)P(4,0)或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)求点A坐标,令y=0,得A点坐标(6,0),求点B坐标,令x=0,得A点坐标(0,8);(2)由勾股定理可得线段AB=10,由折叠的性质可知![]() ,设
,设![]() ,在
,在![]() 中,由勾股定理可得x值,求出点M坐标用待定系数法可得直线AM的表达式;(3)
中,由勾股定理可得x值,求出点M坐标用待定系数法可得直线AM的表达式;(3)
解:(1)y=-![]() x+8
x+8
令![]() 则
则![]() ,
,
令![]() ,则
,则![]()
![]()
(2)由(1)知![]() ,由勾股定理得
,由勾股定理得![]() ,
,
由折叠的性质可知![]() ,
,
设![]() ,则
,则![]()
在![]() 中,根据勾股定理得
中,根据勾股定理得![]()
解得 ![]()
![]()
设直线AM的表达式为![]()
则![]() ,解得
,解得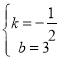
所以直线AM的表达式为![]() .
.
(3)由(2)知![]() ,可得
,可得![]()
①以点M为圆心,![]() 长为半径画圆交x轴于一点P,此时
长为半径画圆交x轴于一点P,此时![]()
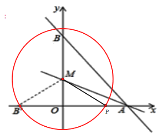
可得![]() ,所以P(4,0);
,所以P(4,0);
②以点![]() 为圆心,
为圆心,![]() 长为半径画圆交x轴于一点P,此时
长为半径画圆交x轴于一点P,此时![]()
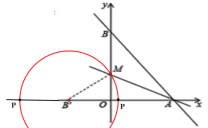
![]() 或1,所以
或1,所以![]() 或
或![]() ;
;
作线段![]() 的垂直平分线交x轴于一点P,此时
的垂直平分线交x轴于一点P,此时![]()
设![]() ,则
,则 ![]() ,根据勾股定理得
,根据勾股定理得![]() ,解得
,解得![]()
所以![]() .
.
综合上述,点P的坐标为P(4,0)或![]() 或
或![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,点D在AB上,DE⊥EB.
(1)求证:AC是△BDE的外接圆的切线;
(2)若AD=2
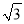 ,AE=6,求EC的长.
,AE=6,求EC的长.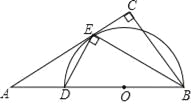
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+2x+c的图象与x轴交于点A(﹣1,0)和点B,与y轴交于点C(0,3).
(1)求该二次函数的表达式;
(2)过点A的直线AD∥BC且交抛物线于另一点D,求直线AD的函数表达式;
(3)在(2)的条件下,请解答下列问题:
①在x轴上是否存在一点P,使得以B、C、P为顶点的三角形与△ABD相似?若存在,求出点P的坐标;若不存在,请说明理由;
②动点M以每秒1个单位的速度沿线段AD从点A向点D运动,同时,动点N以每秒
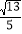 个单位的速度沿线段DB从点D向点B运动,问:在运动过程中,当运动时间t为何值时,△DMN的面积最大,并求出这个最大值.
个单位的速度沿线段DB从点D向点B运动,问:在运动过程中,当运动时间t为何值时,△DMN的面积最大,并求出这个最大值.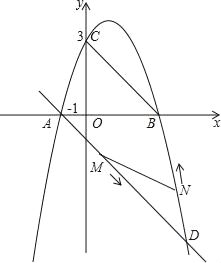
-
科目: 来源: 题型:
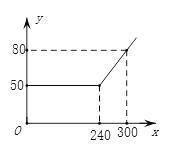
查看答案和解析>>【题目】某网络公司推出了一系列上网包月业务,其中的一项业务是10M40元包240小时,且其中每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,小刚和小明家正好选择了这项上网业务.
(1)当x≥240时,求y与x之间的函数关系式;
(2)若小刚家10月份上网200小时,则他家应付多少元上网费?
(3)若小明家10月份上网费用为62元,则他家该月的上网时间是多少小时?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(阅读理解)
截长补短法,是初中数学儿何题中一种输助线的添加方法,截长就是在长边上载取一条线段与某一短边相等,补短是通过在一条短边上延长一条线段与另一短边相等,从而解决问题.
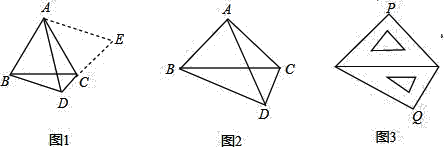
(1)如图1,△ABC是等边三角形,点D是边BC下方一点,∠BDC=120°,探索线段DA、DB、DC之间的数量关系.
解题思路:延长DC到点E,使CE=BD.连接AE,根据∠BAC+∠BDC=180°,可证∠ABD=∠ACE,易证得△ABD≌△ACE,得出△ADE是等边三角形,所以AD=DE,从而探寻线段DA、DB、DC之间的数量关系.
根据上述解题思路,请直接写出DA、DB、DC之间的数量关系是___________
(拓展延伸)
(2)如图2,在Rt△ABC中,∠BAC=90°,AB=AC.若点D是边BC下方一点,∠BDC=90°,探索线段DA、DB、DC之间的数量关系,并说明理由;
(知识应用)
(3)如图3,一副三角尺斜边长都为14cm,把斜边重叠摆放在一起,则两块三角尺的直角项点之间的距离PQ的长为________cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D在线段BC上,若BC=DE,AC=DC,AB=EC,且∠ACE=180°—∠ABC—2x°,则下列角中,大小为x°的角是

A.∠EFCB.∠ABCC.∠FDCD.∠DFC
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 ,
, 是关于
是关于 的一元二次方程
的一元二次方程 的两实根,
的两实根, 的最小值是________.
的最小值是________.
相关试题

