【题目】在△ABC中,∠C=90°,D是边BC上一点,连接AD,若∠BAD+3∠CAD=90°,DC=a,BD=b,则AB=________. (用含a,b的式子表示)
参考答案:
【答案】2a+b.
【解析】
延长BC至点E,使CE=CD=a,连接AE,利用∠BAD+3∠CAD=90°,∠CAB+∠B=90°,证得∠B=2∠CAD,再利用CE=CD,AC⊥CD,证得△AED是等腰三角形,推出∠E=∠EAB,
由此得到AB=EB=2a+b.
如图,延长BC至点E,使CE=CD,连接AE,
∵∠ACB=90°,
∴∠CAB+∠B=90°,AC⊥CD,
∵∠BAD+3∠CAD=90°,∠BAD+∠CAD=∠BAC,
∴∠B=2∠CAD,
∵CE=CD,AC⊥CD,
∴AC垂直平分ED,
∴AE=AD,即△AED是等腰三角形,
∴∠EAC=∠CAD,
∴∠EAD=2∠CAD=∠B,
∴∠EAB=∠B+∠BAD,
∵∠E=∠ADE=∠B+∠BAD,
∴∠E=∠EAB,
∴AB=EB,
∵EB=EC+CD+BD=a+a+b=2a+b,
∴AB=2a+b.
故填:2a+b.

-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 ,
, 是关于
是关于 的一元二次方程
的一元二次方程 的两实根,
的两实根, 的最小值是________.
的最小值是________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在
 中,
中, ,
, ,
, ,点
,点 、
、 同时由
同时由 、
、 两点分别沿
两点分别沿 、
、 方向向点
方向向点 匀速移动,它们的速度都是
匀速移动,它们的速度都是 ,设
,设 秒后
秒后 的面积为
的面积为 面积的一半.则方程(一般形式)为:________.
面积的一半.则方程(一般形式)为:________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知锐角∠MPN,依照下列步骤进行尺规作图:
(1)在射线PN上截取线段PA;
(2)分别以P,A为圆心,大于
 PA的长为半径作弧,两弧相交于E,F两点;
PA的长为半径作弧,两弧相交于E,F两点;(3)作直线EF,交射线PM于点B;
(4)在射线AN上截取AC=PB;
(5)连接BC.
则∠BCP与∠MPN之间的数量关系是_______________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(1,1),B(-1,1),C(0,4).
(1)在平面直角坐标系中描出A,B,C三点;
(2)在同一平面内,点与三角形的位置关系有三种:点在三角形内、点在三角形边上、 点在三角形外.若点P在△ABC外,请判断点P关于y轴的对称点P′与△ABC的位置关系,直接写出判断结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场购进一种单价为
 元的篮球,如果以单价
元的篮球,如果以单价 元出售,那么每月可售出
元出售,那么每月可售出 个,根据销售经验,售价每提高
个,根据销售经验,售价每提高 元,销售量相应减少
元,销售量相应减少 个;
个;某商场购进一种单价为
 元的篮球,如果以单价
元的篮球,如果以单价 元出售,那么每月可售出
元出售,那么每月可售出 个,根据销售经验,售价每提高
个,根据销售经验,售价每提高 元,销售量相应减少
元,销售量相应减少 个;
个; 假设销售单价提高
假设销售单价提高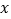 元,那么销售每个篮球所获得的利润是________元;这种篮球每月的销售量是________个;(用含
元,那么销售每个篮球所获得的利润是________元;这种篮球每月的销售量是________个;(用含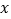 的代数式表示)
的代数式表示) 若商店准备获利
若商店准备获利 元,则销售定价为多少元?商店应进货多少个?
元,则销售定价为多少元?商店应进货多少个? -
科目: 来源: 题型:
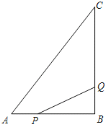
查看答案和解析>>【题目】如图所示,
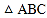 中,
中,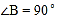 ,
,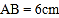 ,
,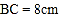 .
.
 点
点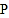 从点
从点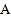 开始沿
开始沿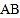 边向
边向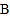 以
以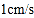 的速度移动,点
的速度移动,点 从
从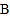 点开始沿
点开始沿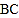 边向点
边向点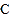 以
以 的速度移动.如果
的速度移动.如果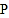 、
、 分别从
分别从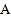 ,
,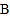 同时出发,线段
同时出发,线段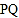 能否将
能否将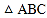 分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
分成面积相等的两部分?若能,求出运动时间;若不能说明理由. 若
若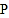 点沿射线
点沿射线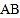 方向从
方向从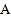 点出发以
点出发以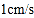 的速度移动,点
的速度移动,点 沿射线
沿射线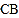 方向从
方向从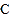 点出发以
点出发以 的速度移动,
的速度移动,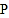 、
、 同时出发,问几秒后,
同时出发,问几秒后,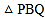 的面积为
的面积为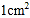 ?
?
相关试题

