搜索
【题目】如图，直线y= 
x+2与双曲线相交于点A（m，3），与x轴交于点C．
（1）求双曲线解析式；
（2）点P在x轴上，如果△ACP的面积为3，求点P的坐标．
参考答案：
【答案】
（1）
解：把A（m，3）代入直线解析式得：3= 
m+2，即m=2，
∴A（2，3），
把A坐标代入y= 
，得k=6，
则双曲线解析式为y= 
（2）
解：对于直线y= x+2，令y=0，得到x=﹣4，即C（﹣4，0），
设P（x，0），可得PC=|x+4|，
∵△ACP面积为3，
∴ |x+4|3=3，即|x+4|=2，
解得：x=﹣2或x=﹣6，
则P坐标为（﹣2，0）或（﹣6，0）．
【解析】（1）把A坐标代入直线解析式求出m的值，确定出A坐标，即可确定出双曲线解析式；（2）设P（x，0），表示出PC的长，高为A纵坐标，根据三角形ACP面积求出x的值，确定出P坐标即可．此题考查了反比例函数与一次函数的交点问题，涉及的知识有：待定系数法确定函数解析式，坐标与图形性质，以及三角形面积求法，熟练掌握待定系数法是解本题的关键．
-
科目： 来源： 题型：
查看答案和解析>>【题目】点E为正方形ABCD边BC上的一点，点G为BC延长线一点，连接AE，过点E作AE⊥EF，且AE=EF，连接CF．
（1）如图1，求证：∠FCG=45°，
（2）如图2，过点D作DH//EF交AB于点H，连接HE，求证：
；（3）如图3，连接AF、DF，若AF交CD于点M，DM=2，BH=3，求DF的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，一次函数y=kx+b（k≠0）的图象与反比例函数y=
（m≠0）的图象交于A、B两点，与x轴交于C点，点A的坐标为（n，6），点C的坐标为（﹣2，0），且tan∠ACO=2． 
（1）求该反比例函数和一次函数的解析式；
（2）求点B的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数y=kx+b（k＜0）与反比例函数y=
的图象相交于A、B两点，一次函数的图象与y轴相交于点C，已知点A（4，1）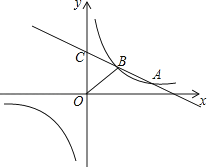 
（1）求反比例函数的解析式；
（2）连接OB（O是坐标原点），若△BOC的面积为3，求该一次函数的解析式． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，O为坐标原点，△ABO的边AB垂直与x轴，垂足为点B，反比例函数y=
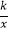（x＞0）的图象经过AO的中点C，且与AB相交于点D，OB=4，AD=3，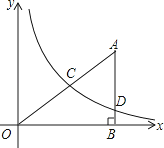 
（1）求反比例函数y=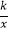 的解析式；
（2）求cos∠OAB的值；
（3）求经过C、D两点的一次函数解析式． -
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系之中，点O为坐标原点，直线
分别交x、y轴于点B、A，直线
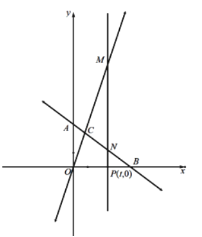
与直线交于点C．（1）如图1，求点C的坐标．
（2）如图2，点P（t，0）为C点的右侧x轴上一点，过点P作x轴垂线分别交AB、OC于点N、M，若MN=5NP，求t的值．
（3）如图3，点F为平面内任意一点，是否存在y轴正半轴上一点E，使点E、F、M、N围成的四边形为菱形，若存在求出点E坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，一次函数y=ax+b（a≠0）的图形与反比例函数y=
（k≠0）的图象交于第二、四象限内的A、B两点，与y轴交于C点，过点A作AH⊥y轴，垂足为H，OH=3，tan∠AOH= 
，点B的坐标为（m，﹣2）． 
（1）求△AHO的周长；
（2）求该反比例函数和一次函数的解析式．
相关试题
