搜索
【题目】在平面直角坐标系中，一次函数y=ax+b（a≠0）的图形与反比例函数y= 
（k≠0）的图象交于第二、四象限内的A、B两点，与y轴交于C点，过点A作AH⊥y轴，垂足为H，OH=3，tan∠AOH= 
，点B的坐标为（m，﹣2）． 
（1）求△AHO的周长；
（2）求该反比例函数和一次函数的解析式．
参考答案：
【答案】
（1）
解：由OH=3，tan∠AOH= 
，得
AH=4．即A（﹣4，3）．
由勾股定理，得
AO= 
=5，
△AHO的周长=AO+AH+OH=3+4+5=12
（2）
解：将A点坐标代入y= 
（k≠0），得
k=﹣4×3=﹣12，
反比例函数的解析式为y= 
；
当y=﹣2时，﹣2= ，解得x=6，即B（6，﹣2）．
将A、B点坐标代入y=ax+b，得
，
解得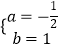 
，
一次函数的解析式为y=﹣ 
x+1．
【解析】（1）根据正切函数，可得AH的长，根据勾股定理，可得AO的长，根据三角形的周长，可得答案；（2）根据待定系数法，可得函数解析式．本题考查了反比例函数与一次函数的交点问题，利用待定系数法是解题关键．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y=
x+2与双曲线相交于点A（m，3），与x轴交于点C．
（1）求双曲线解析式；
（2）点P在x轴上，如果△ACP的面积为3，求点P的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，O为坐标原点，△ABO的边AB垂直与x轴，垂足为点B，反比例函数y=
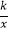（x＞0）的图象经过AO的中点C，且与AB相交于点D，OB=4，AD=3，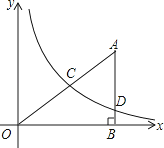 
（1）求反比例函数y=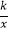 的解析式；
（2）求cos∠OAB的值；
（3）求经过C、D两点的一次函数解析式． -
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系之中，点O为坐标原点，直线
分别交x、y轴于点B、A，直线
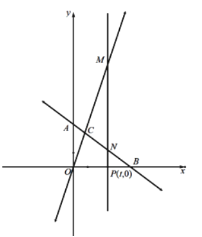
与直线交于点C．（1）如图1，求点C的坐标．
（2）如图2，点P（t，0）为C点的右侧x轴上一点，过点P作x轴垂线分别交AB、OC于点N、M，若MN=5NP，求t的值．
（3）如图3，点F为平面内任意一点，是否存在y轴正半轴上一点E，使点E、F、M、N围成的四边形为菱形，若存在求出点E坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，点O是等边三角形ABC的中心，射线OE交AB边于点E，OF交BC边于点F，若△ABC的面积为S，∠EOF＝120°，则当∠EOF绕点O旋转时，得到的阴影面积发生变化吗？下面有三名同学提出了各自的观点．
甲：阴影部分的面积会发生变化，且当OE，OF分别与△ABC的边垂直时，阴影部分的面积最小．
乙：阴影部分的面积会发生变化，且当E，F分别与△ABC的顶点重合时，阴影部分的面积最大．
丙：无论怎样旋转，阴影部分的面积都保持不变．
你支持谁的观点？____________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图是一块地，已知
，
，
，
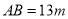，且
（1）求
的长（连接）．（2）证明
是直角三角形．（3）求这块地
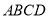的面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】某数学兴趣小组在全校范围内随机抽取了50名同学进行“我最喜爱的卢龙特产”调查活动.
调查问卷
在下面四种卢龙特产中，你最喜爱的是( )(单选)
A．段家沟李子 B．石门核桃
C．鲍子沟葡萄 D．火炉烤白薯
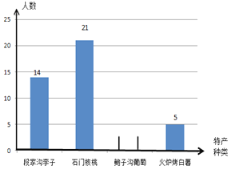
将调查问卷整理后绘制成如图所示的不完整条形统计图：
请根据所给信息解答以下问题：
(1)请补全条形统计图；
(2)若全校有2000名同学，请估计全校同学中最喜爱“段家沟李子”的同学有多少人？
相关试题
