搜索
【题目】如图，在平面直角坐标系中，一次函数y=kx+b（k≠0）的图象与反比例函数y= 
（m≠0）的图象交于A、B两点，与x轴交于C点，点A的坐标为（n，6），点C的坐标为（﹣2，0），且tan∠ACO=2． 
（1）求该反比例函数和一次函数的解析式；
（2）求点B的坐标．
参考答案：
【答案】
（1）解：过点A作AD⊥x轴，垂足为D
由A（n，6），C（﹣2，0）可得，
OD=n，AD=6，CO=2
∵tan∠ACO=2
∴ 
=2，即 
=2
∴n=1
∴A（1，6）
将A（1，6）代入反比例函数，得m=1×6=6
∴反比例函数的解析式为 
将A（1，6），C（﹣2，0）代入一次函数y=kx+b，可得
解得 
∴一次函数的解析式为y=2x+4
（2）解：由 
可得 
解得x1=1，x2=﹣3
∵当x=﹣3时，y=﹣2
∴点B坐标为（﹣3，﹣2）
【解析】本题主要考查了反比例函数与一次函数的交点问题，解决问题的关键是掌握待定系数法求函数解析式．求反比例函数与一次函数的交点坐标时，把两个函数关系式联立成方程组求解，若方程组有解，则两者有交点，若方程组无解，则两者无交点．（1）先过点A作AD⊥x轴，根据tan∠ACO=2，求得点A的坐标，进而根据待定系数法计算两个函数解析式；（2）先联立两个函数解析式，再通过解方程求得交点B的坐标即可．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（题文）如图，说出这个图形的旋转中心，它绕旋转中心至少旋转多大角度才能与原来图形重合？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y=x+1与y轴交于A点，与反比例函数y=
（x＞0）的图象交于点M，过M作MH⊥x轴于点H，且tan∠AHO=
．
（1）求k的值；
（2）设点N（1，a）是反比例函数y=（x＞0）图象上的点，在y轴上是否存在点P，使得PM+PN最小？若存在，求出点P的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】点E为正方形ABCD边BC上的一点，点G为BC延长线一点，连接AE，过点E作AE⊥EF，且AE=EF，连接CF．
（1）如图1，求证：∠FCG=45°，
（2）如图2，过点D作DH//EF交AB于点H，连接HE，求证：
；（3）如图3，连接AF、DF，若AF交CD于点M，DM=2，BH=3，求DF的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数y=kx+b（k＜0）与反比例函数y=
的图象相交于A、B两点，一次函数的图象与y轴相交于点C，已知点A（4，1）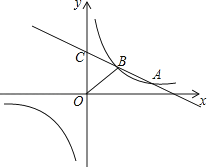 
（1）求反比例函数的解析式；
（2）连接OB（O是坐标原点），若△BOC的面积为3，求该一次函数的解析式． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y=
x+2与双曲线相交于点A（m，3），与x轴交于点C．
（1）求双曲线解析式；
（2）点P在x轴上，如果△ACP的面积为3，求点P的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，O为坐标原点，△ABO的边AB垂直与x轴，垂足为点B，反比例函数y=
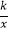（x＞0）的图象经过AO的中点C，且与AB相交于点D，OB=4，AD=3，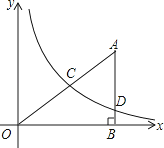 
（1）求反比例函数y=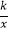 的解析式；
（2）求cos∠OAB的值；
（3）求经过C、D两点的一次函数解析式．
相关试题
