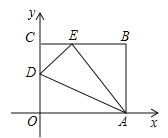
【题目】如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D、E两点的坐标.
参考答案:
【答案】D点坐标为(0,5)、E点坐标为(4,8).
【解析】
试题分析:先根据勾股定理求出BE的长,进而可得出CE的长,求出E点坐标,在Rt△DCE中,由DE=OD及勾股定理可求出OD的长,进而得出D点坐标.
试题解析:依题意可知,折痕AD是四边形OAED的对称轴,
∴在Rt△ABE中,AE=AO=10,AB=8,BE=![]() ,
,
∴CE=4,
∴E(4,8).
在Rt△DCE中,DC2+CE2=DE2,
又∵DE=OD,
∴(8-OD)2+42=OD2,
∴OD=5,
∴D(0,5),
综上D点坐标为(0,5)、E点坐标为(4,8).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场统计了每个营业员在某月的销售额,绘制了如下的条形统计图以及不完整的扇形统计图:

解答下列问题:
(1)设营业员的月销售额为x(单位:万元),商场规定:当x<15时为不称职,当15≤x<20时,为基本称职,当20≤x<25为称职,当x≥25时为优秀.则扇形统计图中的a=________,b=________.
(2)所有营业员月销售额的中位数和众数分别是多少?
(3)为了调动营业员的积极性,决定制定一个月销售额奖励标准,凡到达或超过这个标准的营业员将受到奖励.如果要使得营业员的半数左右能获奖,奖励标准应定为多少万元?并简述其理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图所示的一块地,已知AD=12米,CD=9米,∠ADC=90
 ,AB=39米,BC=36米,求这块地的面积.
,AB=39米,BC=36米,求这块地的面积.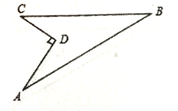
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了了解初三年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.

解答下列问题:
(1)这次抽样调查的样本容量是 ,并补全频数分布直方图;
(2)C组学生的频率为 ,在扇形统计图中D组的圆心角是 度;
(3)请你估计该校初三年级体重超过60kg的学生大约有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】用适当的方法解一元二次方程
(1)x2+3x+1=0
(2)(x﹣1)(x+2)=2(x+2) -
科目: 来源: 题型:
查看答案和解析>>【题目】某运动品牌店对第一季度A,B两款运动鞋的销售情况进行统计,两款运动鞋的销售量及总销售额如图所示:
A,B两款运动鞋销售量统计图 A,B两款运动鞋总销售额统计图
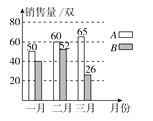
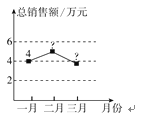
(1)一月份B款运动鞋的销售量是A款的
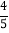 ,则一月份B款运动鞋销售了多少双?
,则一月份B款运动鞋销售了多少双?(2)已知B款运动鞋500元/双,第一季度这两款运动鞋的销售单价保持不变,求二、三月份的总销售额(销售额=销售单价×销售量);
(3)结合第一季度的销售情况,请你对这两款运动鞋的进货、销售等方面提出一条建议.
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知一元二次方程x2﹣3x+m﹣1=0.
(1)若方程有两个不相等的实数根,求实数m的取值范围;
(2)若方程有两个相等的实数根,求此时方程的根.
相关试题

