【题目】![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为直线
为直线![]() 上一动点(点
上一动点(点![]() 不与
不与![]() ,
,![]() 重合),以
重合),以![]() 为边在
为边在![]() 右侧作正方形
右侧作正方形![]() ,连接
,连接![]() .
.
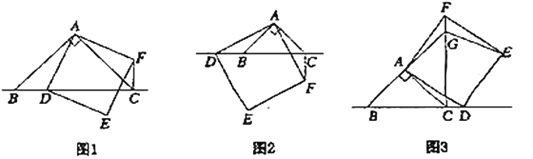
(1)观察猜想:如图1,当点![]() 在线段
在线段![]() 上时,
上时,
①![]() 与
与![]() 的位置关系为:______.②
的位置关系为:______.②![]() ,
,![]() ,
,![]() 之间的数量关系为:______;(将结论直接写在横线上)
之间的数量关系为:______;(将结论直接写在横线上)
(2)数学思考:如图2,当点![]() 在线段
在线段![]() 的延长线上时,(1)中的结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
的延长线上时,(1)中的结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸:如图3,当点![]() 在线段
在线段![]() 的延长线上时,延长
的延长线上时,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .若已知
.若已知![]() ,
,![]() ,请直接写出
,请直接写出![]() 的长.
的长.
参考答案:
【答案】观察猜想:(1)①![]() ; ②
; ②![]() ;数学思考:(2)结论①
;数学思考:(2)结论①![]() 仍然成立,见解析,结论②变为
仍然成立,见解析,结论②变为![]() ,见解析;拓展延伸:(3)
,见解析;拓展延伸:(3)![]() .
.
【解析】
(1)根据正方形的性质证明△DAB≌△FAC,根据全等三角形的性质即可得到结论;
(2)根据正方形的性质证明△DAB≌△FAC,再根据等腰直角三角形的性质即可求解;
(3)分别过点![]() 、
、![]() 作垂线,根据(1)(2)的结论,再证明
作垂线,根据(1)(2)的结论,再证明![]() ,根据勾股定理即可求解.
,根据勾股定理即可求解.
解:(1)在正方形ADEF中,AD=AF,
∵∠BAC=∠DAF=90°,
∴∠BAD=∠CAF,故△DAB≌△FAC
∴∠B=∠ACF,∴∠ACB+∠ACF=90°,即
![]()
②∵△DAB≌△FAC
∴CF=BD,
∵BC=BD+CD,
∴BC=CF+CD
(2)结论①![]() 仍然成立,结论②变为
仍然成立,结论②变为![]() .
.
证明:∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
又![]() ,
,
∴![]() .
.
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() .
.
设![]() 与
与![]() 交于点
交于点![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() 即
即![]()
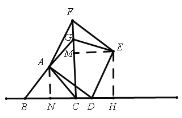
(3)分别过点![]() 、
、![]() 作垂线,类比(1)(2)结论可知
作垂线,类比(1)(2)结论可知![]() ,
,![]() ,
,![]() ,
,
又AD=DE,∠AND=∠DHE=90°,
∵∠NAD+∠ADN=90°,∠EDH+∠ADN=90°,
∴∠NAD=∠EDH
∴![]()
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由勾股定理得![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰△ABC中,AB=AC,∠ACB=72°,

(1)若BD⊥AC于D,求∠ABD的度数;
(2)若CE平分∠ACB,求证:AE=BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.

(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;②当AM的值为 时,四边形AMDN是菱形。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场购进甲、乙两种空调共40台.已知购进一台甲种空调比购进一台乙种空调进价多0.2万元;用36万元购进乙种空调数量是用18万元购进甲种空调数量的4倍.请解答下列问题:
(1)求甲、乙两种空调每台进价各是多少万元?
(2)若商场预计投入资金不多于11.5万元用于购买甲、乙两种空调,且购进甲种空调至少14台,商场有哪几种购进方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知一次函数
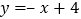 的图象与过
的图象与过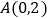 、
、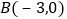 的直线交于点P,与x轴、y轴分别相交于点C和点D.
的直线交于点P,与x轴、y轴分别相交于点C和点D.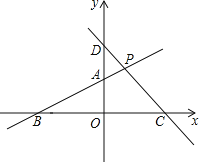
 求直线AB的解析式及点P的坐标;
求直线AB的解析式及点P的坐标; 连接AC,求
连接AC,求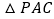 的面积;
的面积; 设点E在x轴上,且与C、D构成等腰三角形,请直接写出点E的坐标.
设点E在x轴上,且与C、D构成等腰三角形,请直接写出点E的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明星期天从家里出发骑车去舅舅家做客,当他骑了一段路时,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后又继续骑车去舅舅家,以下是他本次去舅舅家所用的时间与路程的关系式示意图,根据图中提供的信息回答下列问题:
(1)小明家到舅舅家的路程是______米,小明在商店停留了______分钟;
(2)在整个去舅舅家的途中哪个时间段小明骑车速度最快,最快的速度是多少米/
分?
(3)本次去舅舅家的行程中,小明一共行驶了多少米?一共用了多少分钟?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某一天,水果经营户老张用1600元从水果批发市场批发猕猴桃和芒果共50千克,后再到水果市场去卖,已知猕猴桃和芒果当天的批发价和零售价如表所示:
品名
猕猴桃
芒果
批发价
 元
元 千克
千克
20
40
零售价
 元
元 千克
千克
26
50
 他购进的猕猴桃和芒果各多少千克?
他购进的猕猴桃和芒果各多少千克? 如果猕猴桃和芒果全部卖完,他能赚多少钱?
如果猕猴桃和芒果全部卖完,他能赚多少钱?
相关试题

