【题目】在△ABC中,CA=CB,在△AED中, DA=DE,点D、E分别在CA、AB上.
(1)如图①,若∠ACB=∠ADE=90°,则CD与BE的数量关系是 ;
(2)若∠ACB=∠ADE=120°,将△AED绕点A旋转至如图②所示的位置,求CD与BE的数量关系;
(3)若∠ACB=∠ADE=2α(0°< α < 90°),将△AED绕点A旋转至如图③所示的位置,探究线段CD与BE的数量关系,并加以证明(用含α的式子表示).

参考答案:
【答案】(1)BE=![]() CD;(2)BE=
CD;(2)BE=![]() CD;(3)BE=2CD·sinα,证明见解析.
CD;(3)BE=2CD·sinα,证明见解析.
【解析】试题分析:(1)由已知,△ADE和△ACB都是等腰直角三角形,所以有AE=![]() AD,AB=
AD,AB=![]() AC,从而有
AC,从而有![]() ,即BE=
,即BE=![]() CD.
CD.
(2)如图,分别过点C、D作CM⊥AB于点M,DN⊥AE于点N,
∵CA=CB,DA=DE,∠ACB=∠ADE=120°,
∴∠CAB=∠DAE,∠ACM=∠ADN="60°" ,AM=![]() AB,AN=
AB,AN=![]() AE.
AE.
∴∠CAD=∠BAE.
在Rt△ACM和Rt△ADN中,sin∠ACM=![]() =
=![]() ,sin∠ADN=
,sin∠ADN=![]() =
=![]() ,
,
∴![]() .∴
.∴![]() .
.
又∵∠CAD=∠BAE,∴△BAE∽△CAD.∴![]() .∴BE=
.∴BE=![]() CD.
CD.

(3)根据等腰三角形的性质和锐角三角函数定义求得![]() ,再由△BAE∽△CAD得出
,再由△BAE∽△CAD得出![]() ,从而得出结论.
,从而得出结论.
(1)BE=![]() CD.
CD.
(2)BE=![]() CD.
CD.
(3)BE=2CD·sinα.证明如下:
如图,分别过点C、D作CM⊥AB于点M,DN⊥AE于点N,
∵CA=CB,DA=DE,∠ACB=∠ADE="2α" ,
∴∠CAB=∠DAE,∠ACM=∠ADN="α" ,AM=![]() AB,AN=
AB,AN=![]() AE.
AE.
∴∠CAD=∠BAE.
在Rt△ACM和Rt△ADN中,sin∠ACM=![]() ,sin∠ADN=
,sin∠ADN=![]() ,
,
∴![]() .∴
.∴![]() .
.
又∵∠CAD=∠BAE,∴△BAE∽△CAD.∴![]() .
.
∴BE=2DC·sinα.

-
科目: 来源: 题型:
查看答案和解析>>【题目】对于二次函数y=(x-1)2+2的图象,下列说法正确的是( )
A. 开口向下 B. 当x=-1,时,y有最大值是2 C. 对称轴是x=-1 D. 顶点坐标是(1,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某次考试中,某班级的数学成绩统计图如下.下列说法错误的是( )

A.得分在70~80分之间的人数最多
B.该班的总人数为40
C.得分在90~100分之间的人数最少
D.及格(≥60分)人数是26 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,己知 AB∥CD,∠BAD 和∠BCD 的平分线交于点E,∠1=100°,∠BAD=m°,则∠AEC的度数为( )

A.m°
B.(40+ )°
)°
C.(40﹣ )°
)°
D.(50+ )°
)° -
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式
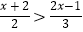 并把解集在数轴上表示出来.
并把解集在数轴上表示出来. -
科目: 来源: 题型:
查看答案和解析>>【题目】苹果的单价为a元/千克,香蕉的单价为b元/千克,买2千克苹果和3千克香蕉共需( )
A.(a+b)元
B.(3a+2b)元
C.(2a+3b)元
D.5(a+b)元 -
科目: 来源: 题型:
查看答案和解析>>【题目】若m、n是一元二次方程x2﹣5x+2=0的两个实数根,则m+n﹣mn的值是( )
A.7
B.﹣7
C.3
D.﹣3
相关试题

